Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kye, Seung-Hyeok
1986.
Subhomogeneous AF 𝐶*-algebras and their Fubini products. II.
Proceedings of the American Mathematical Society,
Vol. 97,
Issue. 2,
p.
244.
Shtern, A. I.
1987.
Nuclear C*-algebras and related questions.
Journal of Soviet Mathematics,
Vol. 38,
Issue. 2,
p.
1762.
Uuye, Otgonbayar
and
Zacharias, Joachim
2020.
The Fubini Product and Its Applications.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 43,
Issue. 6,
p.
4041.

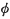 ε
ε 