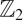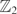Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Hsian-Yang
Lam, Ching Hung
and
Shimakura, Hiroki
2018.
$$\varvec{{\mathbb {Z}}_3}$$
Z
3
-orbifold construction of the Moonshine vertex operator algebra and some maximal 3-local subgroups of the Monster.
Mathematische Zeitschrift,
Vol. 288,
Issue. 1-2,
p.
75.
Chandra, A. Ramesh
and
Mukhi, Sunil
2019.
Curiosities above c = 24.
SciPost Physics,
Vol. 6,
Issue. 5,
Grady, J. Connor
Lam, Ching Hung
Tener, James E.
and
Yamauchi, Hiroshi
2020.
Classification of extremal vertex operator algebras with two simple modules.
Journal of Mathematical Physics,
Vol. 61,
Issue. 5,