Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Andreadakis, S.
1979.
On the automorphism group of free products.
Archiv der Mathematik,
Vol. 32,
Issue. 1,
p.
227.
Noskov, G. A.
Remeslennikov, V. N.
and
Roman'kov, V. A.
1982.
Infinite groups.
Journal of Soviet Mathematics,
Vol. 18,
Issue. 5,
p.
669.
Roman'Kov, Vitaly A.
1992.
Automorphisms of groups.
Acta Applicandae Mathematicae,
Vol. 29,
Issue. 3,
p.
241.
TOLSTYKH, VLADIMIR
2009.
Infinitely generated free nilpotent groups: completeness of the automorphism groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 147,
Issue. 3,
p.
541.
Tolstykh, Vladimir
2011.
Small conjugacy classes in the automorphism groups of relatively free groups.
Journal of Pure and Applied Algebra,
Vol. 215,
Issue. 9,
p.
2086.
ATABEKYAN, V. S.
2013.
THE GROUPS OF AUTOMORPHISMS ARE COMPLETE FOR FREE BURNSIDE GROUPS OF ODD EXPONENTS n ≥ 1003.
International Journal of Algebra and Computation,
Vol. 23,
Issue. 06,
p.
1485.
Kunyavskiĭ, Boris
2013.
Local–global invariants of finite and infinite groups: Around Burnside from another side.
Expositiones Mathematicae,
Vol. 31,
Issue. 3,
p.
256.
Tolstykh, Vladimir
2014.
On the outer automorphism groups of free groups.
Journal of Algebra,
Vol. 420,
Issue. ,
p.
120.
Tolstykh, Vladimir
2015.
Automorphisms of Aut(A),Aa Free Abelian Group.
Communications in Algebra,
Vol. 43,
Issue. 8,
p.
3160.
Serdyukova, Natalia A.
and
Serdyukov, Vladimir I.
2024.
Algebraic Quasi—Fractal Logic of Smart Systems.
Vol. 251,
Issue. ,
p.
163.

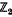 . In this case,
. In this case,