Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T04:27:39.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Braid groups, mapping class groups and their homology with twisted coefficients

Part of: Fiber spaces and bundles Special aspects of infinite or finite groups Homology and cohomology theories

Published online by Cambridge University Press:  05 April 2021

ANDREA BIANCHI
ANDREA BIANCHI*
Affiliation:
Mathematical Institute of the University of Bonn, Endenicher Allee 60, 53115Bonn, Germany. e-mail: bianchi@math.uni-bonn.de Mathematical Institute of the University of Copenhagen, Universitetsparken 5, 2100 Copenhagen, Denmark. e-mail: anbi@math.ku.dk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the Birman–Hilden inclusion 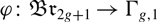$\phi\colon\Br_{2g+1}\to\Gamma_{g,1}$ of the braid group into the mapping class group of an orientable surface with boundary, and prove that 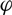$\phi$ is stably trivial in homology with twisted coefficients in the symplectic representation 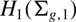$H_1(\Sigma_{g,1})$ of the mapping class group; this generalises a result of Song and Tillmann regarding homology with constant coefficients. Furthermore we show that the stable homology of the braid group with coefficients in 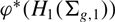$\phi^*(H_1(\Sigma_{g,1}))$ has only 4-torsion.

MSC classification

Primary: 55R20: Spectral sequences and homology of fiber spaces 55R35: Classifying spaces of groups and $H$-spaces 55R37: Maps between classifying spaces 55R40: Homology of classifying spaces, characteristic classes 55R80: Discriminantal varieties, configuration spaces
Secondary: 20F36: Braid groups; Artin groups 55N25: Homology with local coefficients, equivariant cohomology
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 172 , Issue 2 , March 2022 , pp. 249 - 266
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artin, E.. Theorie der Zöpfe. Abhandlungen aus dem Math. Sem. der Univ. Hamburg, 4 (1925), 47–72.CrossRefGoogle Scholar
Bianchi, A.. Embeddings of braid groups into mapping class groups. Master’s thesis, University of Pisa (2016), https://etd.adm.unipi.it/t/etd-06172016-101920/.Google Scholar
Birman, J. and Hilden, H.. On isotopies of homeomorphisms of Riemann surfaces. Ann. of Math. 97 (1973), 424–439.CrossRefGoogle Scholar
Bödigheimer, C. F. and Tillmann, U.. Embeddings of braid groups into mapping class groups and their homology. Configuration Spaces: Geometry, Combinatorics and Topology (2012), 173–191.CrossRefGoogle Scholar
Boldsen, S. K.. Improved homological stability for the mapping class group with integral or twisted coefficients. Math. Zeit. 270 (2012), 297–329.CrossRefGoogle Scholar
Callegaro, F. and Salvetti, M.. Homology of the family of hyperelliptic curves. Israel J. Math. 230 (2019), 653–692.CrossRefGoogle Scholar
Callegaro, F. and Salvetti, M.. Families of superelliptic curves, complex braid groups and generalized dehn twists. Israel J. Math. 238 (2020), 945–1000.CrossRefGoogle Scholar
Earle, C. J. and Schatz, A.. Teichmüller theory for surfaces with boundary. J. Differtial Geom. 4 (1970), 169–185.Google Scholar
Fadell, E. and Neuwirth, L.. Configuration spaces. Math. Scan. 10 (1962), 111–118.CrossRefGoogle Scholar
Farb, B. and Margalit, D.. A Primer on Mapping Class Groups (Princeton University Press, 2012).Google Scholar
Harer, J.. Stability of the homology of the mapping class group of orientable surfaces. Ann. of Math. 121 (1985), 215–249.CrossRefGoogle Scholar
Randal-Williams, O.. Resolutions of moduli spaces and homological stability. J. Eur. Math. Soc. 18 (2016), 1–81.CrossRefGoogle Scholar
Segal, G. and Tillmann, U.. Mapping configuration spaces to moduli spaces. Adv. Stud. in Pure Math. 52 (2008), 469–477.CrossRefGoogle Scholar
Song, Y. and Tillmann, U.. Braids, mapping class groups, and categorical delooping. Math. Ann. 339 (2007), 377–393.CrossRefGoogle Scholar
Vassiliev, V. A.. Complements of discriminants of smooth maps: topology and applications. (AMS, Providence, 1992).CrossRefGoogle Scholar
Vershinin, V. V.. Thom spectra of generalized braid groups. J. London Math. Soc. 61 (2000), 245–258.CrossRefGoogle Scholar