Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-24T06:33:18.214Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization of inverse-closed Beurling classes

Published online by Cambridge University Press:  04 October 2011

Jamil A. Siddiqi  and
Mostefa Ider
Jamil A. Siddiqi
Affiliation:
Département de Mathématiques, Université Laval, Québec G1K 7P4, Canada
Mostefa Ider
Affiliation:
Département de Mathématiques, Université Laval, Québec G1K 7P4, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

In [1], J. Bruna studied the Beurling classes EM(I) of infinitely differentiable functions f defined on an interval I such that for every positive ε, there exists a constant Cε > 0 with the property that

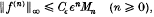
where M = {Mn} is a given sequence of positive numbers. With the hypothesis that the class EM(ℝ) is differentiable, he proved that it is inverse-closed (in the sense that if fεEM(ℝ) and if f is bounded away from zero on ℝ, then its inverse f-1 lies in EM(ℝ)) if and only if the associated sequence A = {An = (Mn/n!)1/n} is almost increasing (i.e. Am ≤ KAn for all m ≤ n, where K > 0 is a constant independent of m and n).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 3 , May 1989 , pp. 495 - 501
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Boman, J. and Hörmander, L.. Classes of infinitely differentiable functions (Mimeographed notes, 1962).Google Scholar
[2] Bruna, J.. On inverse-closed algebras of infinitely differentiable functions. Studia Math. 69 (1980), 61–67.Google Scholar
[3] Korenbljum, B.. Non-triviality conditions for certain classes of functions analytic in an angle and problems of quasi-analyticity. Dokl. Akad. Nauk SSSR 166 (1966), 1046–1049.Google Scholar
[4] Malliavin, P.. Calcul symbolique et sous-algèbres de LI(G). Bull. Soc. Math. France, 87 (1959), 181–190.CrossRefGoogle Scholar
[5] Mandelbrojt, S.. Séries Adhérentes, Régularisation des Suites, Applications (Gauthier-Villars, 1952).Google Scholar
[6] Rudin, W.. Division in algebras of infinitely differentiable functions. J. Math. and Mech. 11 (1962), 797–809.Google Scholar
[7] Siddiqi, J. A. and Ider, M.. Symbolic calculus in analytic Carleman classes, Proc. Amer. Math. Soc. 99 (1987), 347–350.CrossRefGoogle Scholar
[8] Zelazko, W.. Metric Generalizations of Banach Algebras. Rozprawy Matematyczne 47, (PWN, Polish Scientific Publishers, 1965).Google Scholar