Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Atiyah, M. F.
and
Rees, E.
1976.
Vector bundles on projective 3-space.
Inventiones Mathematicae,
Vol. 35,
Issue. 1,
p.
131.
Bukhshtaber, V. M.
1977.
Cobordisms in problems of algebraic topology.
Journal of Soviet Mathematics,
Vol. 7,
Issue. 4,
p.
629.
Grauert, Hans
and
Schneider, Michael
1977.
Komplexe Unterr�ume und holomorphe Vektorraumb�ndel vom Rang zwei.
Mathematische Annalen,
Vol. 230,
Issue. 1,
p.
75.
Barth, W.
and
Elencwajg, G.
1978.
Variétés Analytiques Compactes.
Vol. 683,
Issue. ,
p.
1.
Hartshorne, Robin
1979.
Algebraic vector bundles on projective spaces: A problem list.
Topology,
Vol. 18,
Issue. 2,
p.
117.


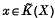 to be less than
to be less than 