Article contents
Complex potential equations II. An application to general relativity
Published online by Cambridge University Press: 24 October 2008
Abstract
The results of a previous paper are applied to a study of the class of Kerr–Schild metrics in general relativity. These metrics have the form
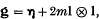
where η is the flat (Minkowski) space-time metric, m is an arbitrary real number, and 1 is a null covector. It is already known that for a certain restricted subclass of these metrics, the vacuum Einstein field equations, viz.
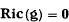
can be written in the form
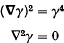
where γ is a complex potential. Using the methods developed in a previous paper, such space-times are characterized by means of a special family of complex surfaces in three-dimensional Euclidean space, and the exact solutions for the metric g are consequently recovered. It is also shown that the field equations for a much wider class of Kerr–Schild metrics can be expressed in terms of a potential formalism, not only in the vacuum case, but also for many electrovacuum solutions.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 80 , Issue 2 , September 1976 , pp. 349 - 355
- Copyright
- Copyright © Cambridge Philosophical Society 1976
References
REFERENCES
- 3
- Cited by


