Article contents
Construction of a family of Moufang loops
Published online by Cambridge University Press: 10 April 2007
Abstract
This paper is an excerpt from a Rayleigh essay submitted at the University of Cambridge in January 1970. We reproduce it now as it gives a general construction of a family of Moufang loops to which all bar one of the finite subloops of the Cayley algebra 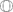 belong. These subloops were classified up to isomorphism in the original essay, but are classified up to equivalence under the action of the group of symmetries of
belong. These subloops were classified up to isomorphism in the original essay, but are classified up to equivalence under the action of the group of symmetries of 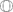 in Boddington and Rumynin [1]. Explicitly, given a group G with an element a such that a2=1 in its centre, we construct a Moufang group
in Boddington and Rumynin [1]. Explicitly, given a group G with an element a such that a2=1 in its centre, we construct a Moufang group 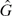 in which G has index 2.
in which G has index 2. 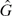 will be non-associative unless G is abelian.
will be non-associative unless G is abelian.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 142 , Issue 2 , March 2007 , pp. 233 - 237
- Copyright
- Copyright © Cambridge Philosophical Society 2007
References
REFERENCES
- 3
- Cited by


