I. The zeros of the function on the line
Published online by Cambridge University Press: 24 October 2008
In this and the succeeding paper I solve two problems suggested by Prof. Hardy, namely (1) that of proving that Ramanujan's function
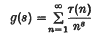
has no zeros on the line 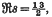 and (2) that of finding an asymptotic formula
and (2) that of finding an asymptotic formula
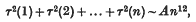
where A is a constant. I also prove similar results concerning the coefficients of general modular forms. I am indebted to Prof. Hardy and Mr Ingham for various suggestions, and in particular to Mr Ingham's paper, “A note on Riemann's ζ-function and Dirichlet's L-functions”.
* Ingham, A. E., J. London. Math. Soc. 5 (1929), 107–12.Google Scholar
† Ramanujan, S., “On certain arithmetical functions”, Collected Papers (Cambridge, 1927), pp. 136–62,Google Scholar or Trans. Cambridge Phil. Soc. 22 (1916), 159–84.Google Scholar
‡ Hardy, G. H., “Note on Ramanujan's function τ(n)”, Proc. Cambridge Phil. Soc. 23 (1927), 675–80.CrossRefGoogle Scholar
* Mordell, L. J., “On Ramanujan's empirical expansions of modular functions”, Proc. Cambridge Phil. Soc. 19 (1920), 117–24.Google Scholar
† This functional equation appears to have been first stated by Wilton, J. R. in “A note on Ramanujan's arithmetical function τ(n)”, Proc. Cambridge Phil. Soc. 25 (1928), 121–9.CrossRefGoogle Scholar Wilton also proves functional equations for more general functions of the form
* Actually ![]() as I prove in my second paper.
as I prove in my second paper.