Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1966.
Lectures on Functional Equations their and Applications.
Vol. 19,
Issue. ,
p.
383.
Harris, Stewart
1967.
Proof that Successive Derivatives of Boltzmann's H Function for a Discrete Velocity Gas Alternate in Sign.
Journal of Mathematical Physics,
Vol. 8,
Issue. 12,
p.
2407.
Rueda, A.
1973.
Entropy production for a near-equilibrium isolated system of thermalizing matter and radiation.
The Journal of Chemical Physics,
Vol. 58,
Issue. 8,
p.
3320.
Nishimura, Shōichi
1974.
Random collision processes with transition probabilities belonging to the same type of distribution.
Journal of Applied Probability,
Vol. 11,
Issue. 4,
p.
703.
Nishimura, Shōichi
1974.
Random collision processes with transition probabilities belonging to the same type of distribution.
Journal of Applied Probability,
Vol. 11,
Issue. 4,
p.
703.
Shōichi, Nishimura
1974.
Random collision processes and their limiting distribution using the discrimination information.
Journal of Applied Probability,
Vol. 11,
Issue. 02,
p.
266.
Shōichi, Nishimura
1974.
Random collision processes and their limiting distribution using the discrimination information.
Journal of Applied Probability,
Vol. 11,
Issue. 2,
p.
266.
Nishimura, Shōichi
1975.
An inequality for a metric in a random collision process.
Journal of Applied Probability,
Vol. 12,
Issue. 2,
p.
239.
Nishimura, Shōichi
1975.
An inequality for a metric in a random collision process.
Journal of Applied Probability,
Vol. 12,
Issue. 2,
p.
239.
Brumat, Carlo
1978.
Irreversibility and entropy.
Rivista di Matematica per le Scienze Economiche e Sociali,
Vol. 1,
Issue. 1,
p.
39.
Yang, Chen Ning
and
Yang, Chen Ping
1980.
DOES VIOLATION OF MICROSCOPIC TIME‐REVERSAL INVARIANCE LEAD TO THE POSSIBILITY OF ENTROPY DECREASE?*.
Transactions of the New York Academy of Sciences,
Vol. 40,
Issue. 1 Series II,
p.
267.
Seneta, E.
1982.
Entropy and martingales in Markov chain models.
Journal of Applied Probability,
Vol. 19,
Issue. A,
p.
367.
Seneta, E.
1982.
Entropy and martingales in Markov chain models.
Journal of Applied Probability,
Vol. 19,
Issue. A,
p.
367.
Mead, C. Alden
1982.
Advances in Chemical Physics.
Vol. 51,
Issue. ,
p.
113.
Hoare, M. R.
1984.
Advances in Chemical Physics.
Vol. 56,
Issue. ,
p.
1.
Cohen, Joel E.
Iwasa, Yoh
Rautu, Gh.
Beth Ruskai, Mary
Seneta, Eugene
and
Zbaganu, Gh.
1993.
Relative entropy under mappings by stochastic matrices.
Linear Algebra and its Applications,
Vol. 179,
Issue. ,
p.
211.
Itoh, Y
and
Cohen, J E
1994.
Competitive ternary interactions and relative entropy of solutions.
Journal of Physics A: Mathematical and General,
Vol. 27,
Issue. 19,
p.
6383.
Triolo, L.
1995.
A generalization of the H‐theorem to steady non‐equilibrium states. Part 1: A basic decomposition and the linear case.
Mathematical Methods in the Applied Sciences,
Vol. 18,
Issue. 7,
p.
507.
1997.
Leading Personalities in Statistical Sciences.
p.
353.
Seneta, E.
2004.
Encyclopedia of Statistical Sciences.
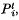 , that the system is in state i after t steps, will converge to non-zero quantities,
, that the system is in state i after t steps, will converge to non-zero quantities, 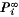 , which are independent of the initial state. This condition of accessibility corresponds, in statistical mechanics, to the condition of ‘metrical transitivity’.
, which are independent of the initial state. This condition of accessibility corresponds, in statistical mechanics, to the condition of ‘metrical transitivity’.

