Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1981.
Von Neumann Algebras.
Vol. 27,
Issue. ,
p.
387.
Jajte, R.
1984.
Probability Measures on Groups VII.
Vol. 1064,
Issue. ,
p.
219.
Jajte, R.
1984.
Probability Theory on Vector Spaces III.
Vol. 1080,
Issue. ,
p.
130.
1985.
Ergodic Theorems.
p.
321.
Hensz, Ewa
and
Jajte, Ryszard
1986.
Pointwise convergence theorems inL 2 over a von Neumann algebra.
Mathematische Zeitschrift,
Vol. 193,
Issue. 3,
p.
413.
1987.
Saks Spaces and Applications to Functional Analysis.
Vol. 139,
Issue. ,
p.
279.
Chilin, Vladimir I.
Medzhitov, Arthur M.
and
Sukochev, Pheodor A.
1989.
Isometries of non-commutative Lorentz spaces.
Mathematische Zeitschrift,
Vol. 200,
Issue. 4,
p.
527.
Dodds, Peter G.
Dodds, Theresa K. -Y.
and
de Pagter, Ben
1989.
Non-commutative Banach function spaces.
Mathematische Zeitschrift,
Vol. 201,
Issue. 4,
p.
583.
Jajte, R.
1989.
Probability Theory on Vector Spaces IV.
Vol. 1391,
Issue. ,
p.
125.
Jajte, Ryszard
1990.
Quantum Probability and Applications V.
Vol. 1442,
Issue. ,
p.
231.
Jajte, Ryszard
1990.
Almost sure convergence of iterates of contractions in noncommutativeL 2-spaces.
Mathematische Zeitschrift,
Vol. 205,
Issue. 1,
p.
165.
Goldstein, M. S.
and
Grabarnik, G. Ya.
1991.
Almost sure convergence theorems in von Neumann algebras.
Israel Journal of Mathematics,
Vol. 76,
Issue. 1-2,
p.
161.
Dodds, Peter G.
Dodds, Theresa K.
and
Pagter, Ben De
1991.
Weakly compact subsets of symmetric operator spaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 110,
Issue. 1,
p.
169.
Dodds, Peter G.
Dodds, Theresa K.
and
de Pagter, Ben
1992.
Fully symmetric operator spaces.
Integral Equations and Operator Theory,
Vol. 15,
Issue. 6,
p.
942.
Chilin, Vladimir I.
Krygin, Andrei V.
and
Sukochev, Pheodor A.
1992.
Extreme points of convex fully symmetric sets of measurable operators.
Integral Equations and Operator Theory,
Vol. 15,
Issue. 2,
p.
186.
Watanabe, Keiichi
1992.
Some results on non-commutative Banach function spaces.
Mathematische Zeitschrift,
Vol. 210,
Issue. 1,
p.
555.
Chilin, Vladimir I.
Krygin, Andrei V.
and
Sukochev, Pheodor A.
1992.
Local uniform and uniform convexity of non-commutative symmetric spaces of measurable operators.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 111,
Issue. 2,
p.
355.
Dodds, Peter G.
Dodds, Theresa K.-Y.
and
de Pagter, Ben
1993.
Noncommutative Köthe duality.
Transactions of the American Mathematical Society,
Vol. 339,
Issue. 2,
p.
717.
Dodds, Peter G.
and
Dodds, Theresa K.-Y.
1995.
SOME ASPECTS OF THE THEORY OF SYMMETRIC OPERATOR SPACES.
Quaestiones Mathematicae,
Vol. 18,
Issue. 1-3,
p.
47.
Grabarnik, Gennady
and
Katz, Alexander
1995.
Ergodic type theorems for finite von Neumann algebras.
Israel Journal of Mathematics,
Vol. 90,
Issue. 1-3,
p.
403.
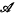 which are linear positive and norm-reducing for both the operator norm ‖ ‖∞ and the integral norm ‖ ‖1 associated with a normal trace ρ on
which are linear positive and norm-reducing for both the operator norm ‖ ‖∞ and the integral norm ‖ ‖1 associated with a normal trace ρ on 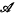 . Here we introduce a class of Banach spaces of unbounded operators, including the Lp spaces defined in (6), in which the transformations α reduce the norm, and in which the mean ergodic theorem holds; that is the averages
. Here we introduce a class of Banach spaces of unbounded operators, including the Lp spaces defined in (6), in which the transformations α reduce the norm, and in which the mean ergodic theorem holds; that is the averages