A family of Fitting classes of supersoluble groups
Published online by Cambridge University Press: 24 October 2008
Extract
A class of groups that is closed with respect to subnormal subgroups and normal products is called a Fitting class. Given a finite soluble group G, one may ask for the Fitting class 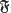 (G) generated by G, that is the intersection of all Fitting classes containing G. For simple or nilpotent groups G it is easy to compute
(G) generated by G, that is the intersection of all Fitting classes containing G. For simple or nilpotent groups G it is easy to compute 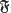 (G), but in other cases the determination of
(G), but in other cases the determination of 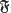 (G) seems to be surprisingly difficult, and there is no general method of solving this problem. In recent years there has been a lot of work in this area, see for instance Bryce and Cossey[l], [2], Hawkes[6] (or [5], IX. 9. Var. II), Heineken[7] and McCann[10].
(G) seems to be surprisingly difficult, and there is no general method of solving this problem. In recent years there has been a lot of work in this area, see for instance Bryce and Cossey[l], [2], Hawkes[6] (or [5], IX. 9. Var. II), Heineken[7] and McCann[10].
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 118 , Issue 1 , July 1995 , pp. 49 - 57
- Copyright
- Copyright © Cambridge Philosophical Society 1995
References
REFERENCES
- 2
- Cited by


