Published online by Cambridge University Press: 06 December 2022
We show that the only finite quasi-simple non-abelian groups that can faithfully act on rationally connected threefolds are the following groups:
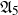 ${\mathfrak{A}}_5$
,
${\mathfrak{A}}_5$
,
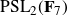 ${\text{PSL}}_2(\textbf{F}_7)$
,
${\text{PSL}}_2(\textbf{F}_7)$
,
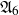 ${\mathfrak{A}}_6$
,
${\mathfrak{A}}_6$
,
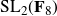 ${\text{SL}}_2(\textbf{F}_8)$
,
${\text{SL}}_2(\textbf{F}_8)$
,
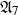 ${\mathfrak{A}}_7$
,
${\mathfrak{A}}_7$
,
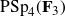 ${\text{PSp}}_4(\textbf{F}_3)$
,
${\text{PSp}}_4(\textbf{F}_3)$
,
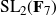 ${\text{SL}}_2(\textbf{F}_{7})$
,
${\text{SL}}_2(\textbf{F}_{7})$
,
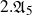 $2.{\mathfrak{A}}_5$
,
$2.{\mathfrak{A}}_5$
,
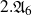 $2.{\mathfrak{A}}_6$
,
$2.{\mathfrak{A}}_6$
,
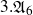 $3.{\mathfrak{A}}_6$
or
$3.{\mathfrak{A}}_6$
or
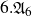 $6.{\mathfrak{A}}_6$
. All of these groups with a possible exception of
$6.{\mathfrak{A}}_6$
. All of these groups with a possible exception of
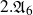 $2.{\mathfrak{A}}_6$
and
$2.{\mathfrak{A}}_6$
and
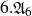 $6.{\mathfrak{A}}_6$
indeed act on some rationally connected threefolds.
$6.{\mathfrak{A}}_6$
indeed act on some rationally connected threefolds.