No CrossRef data available.
General series involving H-functions
Published online by Cambridge University Press: 24 October 2008
Extract
MacRobert (4–7) and Ragab(8) have summed many infinite and finite series of E-functions by expressing the E-functions as Barnes integrals and interchanging the order of summation and integration. Verma (9) has given two general expansions involving E-functions from which, in addition to some new results, all the expansions given by MacRobert and Ragab can be deduced. Proceeding similarly, we have studied general summations involving H-functions. The H-function is the most generalized form of the hypergeometric function. It contains a vast number of well-known analytic functions as special cases and also an important class of symmetrical Fourier kernels of a very general nature. The H-function is defined as (2)
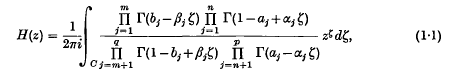
where 0 ≤ n ≤ p, 1 ≤ m ≤ q, αj, βj are positive numbers and aj, bj may be complex numbers.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 65 , Issue 2 , March 1969 , pp. 461 - 465
- Copyright
- Copyright © Cambridge Philosophical Society 1969


