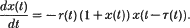Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gopalsamy, K
and
Zhang, B.G
1989.
On delay differential equations with impulses.
Journal of Mathematical Analysis and Applications,
Vol. 139,
Issue. 1,
p.
110.
Gopalsamy, K.
He, Xue‐Zhong
and
Wen, Lizhi
1992.
Global Attractivity and ‘Level‐Crossings’ in a Periodic Logistic Integrodifferential Equation.
Mathematische Nachrichten,
Vol. 156,
Issue. 1,
p.
25.
Yu, Jianshe
Wu, Jianhong
and
Zou, Xingfu
1996.
On a hyperlogistic delay equation.
Glasgow Mathematical Journal,
Vol. 38,
Issue. 2,
p.
255.
Li, Jingwen
1996.
Global attractivity in a generalized delay logistic equation.
Applied Mathematics,
Vol. 11,
Issue. 2,
p.
165.
Stamova, Ivanka M.
and
Stamov, Gani T.
2001.
Lyapunov–Razumikhin method for impulsive functional differential equations and applications to the population dynamics.
Journal of Computational and Applied Mathematics,
Vol. 130,
Issue. 1-2,
p.
163.
Bainov, D. D.
and
Stamova, I. M.
2001.
Vector Lyapunov functions and conditional stability for systems of impulsive differential-difference equations.
The ANZIAM Journal,
Vol. 42,
Issue. 3,
p.
341.
Bainov, D. D.
Dishliev, A. B.
and
Stamova, I. M.
2002.
Practical stability of the solutions of impulsive systems of differential-difference equations via the method of comparison and some applications to population dynamics.
The ANZIAM Journal,
Vol. 43,
Issue. 4,
p.
525.
Stamova, Ivanka M.
2006.
Lyapunov method for boundedness of solutions of nonlinear impulsive functional differential equations.
Applied Mathematics and Computation,
Vol. 177,
Issue. 2,
p.
714.
Sun, Yuan Gong
2007.
Remark on the paper of Park.
Applied Mathematics and Computation,
Vol. 187,
Issue. 2,
p.
1250.
Liang, Ruixi
and
Shen, Jianhua
2007.
Uniform stability theorems for delay differential equations with impulses.
Journal of Mathematical Analysis and Applications,
Vol. 326,
Issue. 1,
p.
62.
Stamova, Ivanka
and
Stamov, Gani
2016.
Applied Impulsive Mathematical Models.
p.
113.