Article contents
Graphs in the plane invariant under an area preserving linear map and general continuous solutions of certain quadratic functional equations
Published online by Cambridge University Press: 24 October 2008
Abstract
The requirement that the graph 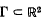 of a function
of a function  be invariant under a linear map
be invariant under a linear map 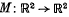 is equivalent to a functional equation of f. For area preserving maps M(det (M) = 1), the functional equation is equivalent to an (easily solved) linear one, or to a quadratic one of the form
is equivalent to a functional equation of f. For area preserving maps M(det (M) = 1), the functional equation is equivalent to an (easily solved) linear one, or to a quadratic one of the form

for all  Here 2C = Trace (M). It is shown that (Q) admits continuous solutions ⇔ M has real eigenvalues ⇔ (Q) has linear solutions f(x) = λx ⇔ |C| ≥ 1. For |c| = 1 or C < – 1, (Q) only admits a few simple solutions. For C > 1, (Q) admits a rich supply of continuous solutions. These are parametrised by an arbitrary function, and described in the sense that a construction is given for the graphs
Here 2C = Trace (M). It is shown that (Q) admits continuous solutions ⇔ M has real eigenvalues ⇔ (Q) has linear solutions f(x) = λx ⇔ |C| ≥ 1. For |c| = 1 or C < – 1, (Q) only admits a few simple solutions. For C > 1, (Q) admits a rich supply of continuous solutions. These are parametrised by an arbitrary function, and described in the sense that a construction is given for the graphs  of the functions which solve (Q).
of the functions which solve (Q).
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 97 , Issue 2 , March 1985 , pp. 261 - 278
- Copyright
- Copyright © Cambridge Philosophical Society 1985
References
REFERENCES
- 2
- Cited by

