Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zalcman, Lawrence
1980.
Offbeat Integral Geometry.
The American Mathematical Monthly,
Vol. 87,
Issue. 3,
p.
161.
Berenstein, Carlos A.
and
Gay, Roger
1986.
A local version of the two-circles theorem.
Israel Journal of Mathematics,
Vol. 55,
Issue. 3,
p.
267.
Berenstein, C. A.
Gay, R.
and
Yger, A.
1990.
Inversion of the local Pompeiu transform.
Journal d'Analyse Mathématique,
Vol. 54,
Issue. 1,
p.
259.
Rana, Inder K.
1990.
Unsmoothing over balls via plane wave decomposition.
Rendiconti del Circolo Matematico di Palermo,
Vol. 39,
Issue. 2,
p.
217.
Zalcman, L.
1992.
Approximation by Solutions of Partial Differential Equations.
p.
185.
Netuka, Ivan
and
Veselý, Jiří
1994.
Classical and Modern Potential Theory and Applications.
p.
359.
Волчков, Валерий Владимирович
and
Volchkov, Valerii Vladimirovich
1997.
Теоремы единственности для некоторых классов функций с нулевыми сферическими средними.
Математические заметки,
Vol. 62,
Issue. 1,
p.
59.
Volchkov, V V
1997.
Solution of the support problem for several function classes.
Sbornik: Mathematics,
Vol. 188,
Issue. 9,
p.
1279.
Volchkov, V. V.
1997.
Uniqueness theorems for some classes of functions with zero spherical means.
Mathematical Notes,
Vol. 62,
Issue. 1,
p.
50.
Волчков, Валерий Владимирович
and
Volchkov, Valerii Vladimirovich
1997.
Решение проблемы носителя для некоторых классов функций.
Математический сборник,
Vol. 188,
Issue. 9,
p.
13.
Волчков, Валерий Владимирович
and
Volchkov, Valerii Vladimirovich
2001.
Окончательный вариант локальной теоремы о двух радиусах на гиперболических пространствах.
Известия Российской академии наук. Серия математическая,
Vol. 65,
Issue. 2,
p.
3.
Zhou, Yiying
2001.
Two Radius Support Theorem for the Sphere Transform.
Journal of Mathematical Analysis and Applications,
Vol. 254,
Issue. 1,
p.
120.
Volchkov, V V
2001.
A definitive version of the local two-radii theorem on hyperbolic spaces.
Izvestiya: Mathematics,
Vol. 65,
Issue. 2,
p.
207.
Волчков, Валерий Владимирович
and
Volchkov, Valerii Vladimirovich
2001.
Теоремы о шаровых средних на симметрических пространствах.
Математический сборник,
Vol. 192,
Issue. 9,
p.
17.
Volchkov, V. V.
2006.
A local two-radii theorem for quasianalytic classes of functions.
Mathematical Notes,
Vol. 80,
Issue. 3-4,
p.
468.
Волчков, Валерий Владимирович
and
Volchkov, Valerii Vladimirovich
2006.
Локальная теорема о двух радиусах для квазианалитических классов функций.
Математические заметки,
Vol. 80,
Issue. 4,
p.
490.
Волчков, Валерий Владимирович
and
Volchkov, Valerii Vladimirovich
2006.
Теоремы единственности для решений уравнения свертки на симметрических пространствах.
Известия Российской академии наук. Серия математическая,
Vol. 70,
Issue. 6,
p.
3.
Ochakovskaya, O. A.
2007.
Liouville-type theorems for functions with zero integrals over balls of fixed radius.
Doklady Mathematics,
Vol. 76,
Issue. 1,
p.
530.
Volchkov, V V
2007.
Local two-radii theorem in symmetric spaces.
Sbornik: Mathematics,
Vol. 198,
Issue. 11,
p.
1553.
Волчков, Валерий Владимирович
and
Volchkov, Valerii Vladimirovich
2007.
Локальная теорема о двух радиусах на симметрических пространствах.
Математический сборник,
Vol. 198,
Issue. 11,
p.
21.
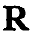 n
n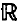 n which is of class Cn and either has zero mean on all spheres of unit radius, or has zero mean in all balls of unit radius admits a unique expansion in terms of eigenfunctions of the Laplacian operator. In a similar manner, a suitably smooth vector-valued function in
n which is of class Cn and either has zero mean on all spheres of unit radius, or has zero mean in all balls of unit radius admits a unique expansion in terms of eigenfunctions of the Laplacian operator. In a similar manner, a suitably smooth vector-valued function in 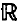 n which has zero flux through all spheres cf unit radius is shown to be decomposable as the sum of a solenoidal part and a series of conservative parts that are eigenfunctions of the Laplacian. Applications are given, including some in complex analysis.
n which has zero flux through all spheres cf unit radius is shown to be decomposable as the sum of a solenoidal part and a series of conservative parts that are eigenfunctions of the Laplacian. Applications are given, including some in complex analysis.

