Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Falconer, K J
1988.
A subadditive thermodynamic formalism for mixing repellers.
Journal of Physics A: Mathematical and General,
Vol. 21,
Issue. 14,
p.
L737.
Zähle, U.
1990.
Self‐Similar Random Measures. II A Generalization to Self‐Affine Measures.
Mathematische Nachrichten,
Vol. 146,
Issue. 3-6,
p.
85.
1991.
Fractal dimensions and spectra of interfaces with application to turbulence.
Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences,
Vol. 435,
Issue. 1895,
p.
505.
Massopust, Peter R.
1991.
Vector—valued fractal interpolation functions and their box dimension.
Aequationes Mathematicae,
Vol. 42,
Issue. 1,
p.
1.
Zähle, U.
1991.
Self‐Similar Random Measures III – Self‐Similar Random Processes.
Mathematische Nachrichten,
Vol. 151,
Issue. 1,
p.
121.
Deliu, Anca
Geronimo, J. S.
Shonkwiler, R.
and
Hardin, D.
1991.
Dimensions associated with recurrent self-similar sets.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 110,
Issue. 2,
p.
327.
Falconer, K. J.
1992.
The dimension of self-affine fractals II.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 111,
Issue. 1,
p.
169.
Gatzouras, Dimitrios
and
Lalley, Steven P.
1994.
Statistically self-affine sets: Hausdorff and box dimensions.
Journal of Theoretical Probability,
Vol. 7,
Issue. 2,
p.
437.
Patzschke, N.
and
Zähle, M.
1994.
Fractional differentiation in the self-affine case. IV — random measures.
Stochastics and Stochastic Reports,
Vol. 49,
Issue. 1-2,
p.
87.
Falconer, K. J.
1994.
Bounded distortion and dimension for non-conformal repellers.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 115,
Issue. 2,
p.
315.
1994.
Fractal Functions, Fractal Surfaces, and Wavelets.
p.
363.
Pollicott, Mark
and
Weiss, Howard
1994.
The dimensions of some self-affine limit sets in the plane and hyperbolic sets.
Journal of Statistical Physics,
Vol. 77,
Issue. 3-4,
p.
841.
Falconer, K. J.
1995.
Sub-self-similar sets.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 8,
p.
3121.
Hueter, Irene
and
Lalley, Steven P.
1995.
Falconer's formula for the Hausdorff dimension of a self-affine set in R2.
Ergodic Theory and Dynamical Systems,
Vol. 15,
Issue. 1,
p.
77.
Hu, Huyi
1996.
Dimensions of invariant sets of expanding maps.
Communications in Mathematical Physics,
Vol. 176,
Issue. 2,
p.
307.
Kenyon, R.
and
Peres, Y.
1996.
Hausdorff dimensions of sofic affine-invariant sets.
Israel Journal of Mathematics,
Vol. 94,
Issue. 1,
p.
157.
Steffen, Klaus
1996.
Felix Hausdorff zum Gedächtnis.
p.
185.
Edalat, Abbas
1997.
Domains for Computation in Mathematics, Physics and Exact Real Arithmetic.
Bulletin of Symbolic Logic,
Vol. 3,
Issue. 4,
p.
401.
Chin, Wai
Hunt, Brian
and
Yorke, James
1997.
Correlation dimension for iterated function systems.
Transactions of the American Mathematical Society,
Vol. 349,
Issue. 5,
p.
1783.
Dihe, Hu
1998.
The classification of statistically recursive sets.
Wuhan University Journal of Natural Sciences,
Vol. 3,
Issue. 3,
p.
270.
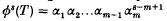 where m is the smallest integer greater than or equal to s. Let T1, …, Tk be contractive linear transformations on ℝn. Let
where m is the smallest integer greater than or equal to s. Let T1, …, Tk be contractive linear transformations on ℝn. Let 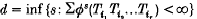 where the sum is over all finite sequences (i1, …, ir) with 1 ≤ ij ≤ k. Then for almost all (a1, …, ak) ∈ ℝnk, the unique non-empty compact set F satisfying
where the sum is over all finite sequences (i1, …, ir) with 1 ≤ ij ≤ k. Then for almost all (a1, …, ak) ∈ ℝnk, the unique non-empty compact set F satisfying 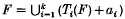 has Hausdorff dimension min{d, n}. Moreover the ‘box counting’ dimension of F is almost surely equal to this number.
has Hausdorff dimension min{d, n}. Moreover the ‘box counting’ dimension of F is almost surely equal to this number.

