No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let the stationary point process N(·) be the mixture of scaled versions of a stationary orderly point process N1(·) of unit intensity with mixing distribution G(·), so that
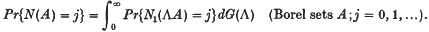
With
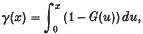
N(·) has finite or infinite intensity as 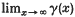 is finite or infinite, and it is Khinchin orderly when the function γ(·) is slowly varying at infinity. Conditions for N(·) to be orderly involve both G(·) and the Palm distribution of N1(·).
is finite or infinite, and it is Khinchin orderly when the function γ(·) is slowly varying at infinity. Conditions for N(·) to be orderly involve both G(·) and the Palm distribution of N1(·).