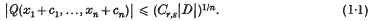No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let Q (x1, …, xn) be a real indefinite quadratic form in n-variables x1,…, xn with signature (r, s),r + s = n and determinant D ≠ 0. Then it is known (see Blaney (2)) that there exists constant Cr, s depending only on r, s such that given any real numbers c1, …,cn we can find integers x1, …, xn satisfying