Published online by Cambridge University Press: 12 June 2013
Let (V,0) be the germ of an analytic variety in 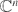 $\mathbb{C}^n$ and f an analytic function germ defined on V. For functions with isolated singularity on V, Bruce and Roberts introduced a generalization of the Milnor number of f, which we call Bruce–Roberts number, μBR(V,f). Like the Milnor number of f, this number shows some properties of f and V. In this paper we investigate algebraic and geometric characterizations of the constancy of the Bruce–Roberts number for families of functions with isolated singularities on V. We also discuss the topological invariance of the Bruce–Roberts number for families of quasihomogeneous functions defined on quasihomogeneous varieties. As application of the results, we prove a relative version of the Zariski multiplicity conjecture for quasihomogeneous varieties.
$\mathbb{C}^n$ and f an analytic function germ defined on V. For functions with isolated singularity on V, Bruce and Roberts introduced a generalization of the Milnor number of f, which we call Bruce–Roberts number, μBR(V,f). Like the Milnor number of f, this number shows some properties of f and V. In this paper we investigate algebraic and geometric characterizations of the constancy of the Bruce–Roberts number for families of functions with isolated singularities on V. We also discuss the topological invariance of the Bruce–Roberts number for families of quasihomogeneous functions defined on quasihomogeneous varieties. As application of the results, we prove a relative version of the Zariski multiplicity conjecture for quasihomogeneous varieties.