Kernels with only a finite number of characteristic values
Published online by Cambridge University Press: 24 October 2008
Extract
Let K(s, t) be a complex-valued L2 kernel on the square ⋜ s, t ⋜ by which we mean
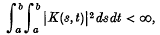
and let {λν}, perhaps empty, be the set of finite characteristic values (f.c.v.) of K(s, t), i.e. complex numbers with which there are associated non-trivial L2 functions øν(s) satisfying
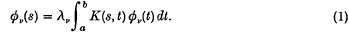
For such kernels, the iterated kernels,
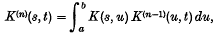
are well-defined (1), as are the higher order traces
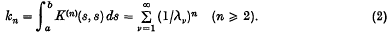
Carleman(2) showed that the f.c.v. of K are the zeros of the modified Fredhoim determinant
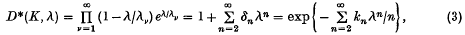
the latter expression holding only for |λ| sufficiently small (3). The δn in (3) may be calculated, at least in theory, by well-known formulae involving the higher order traces (1). For our later analysis of this case, we define 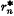 and
and 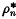 , respectively, as the minimum and maximum moduli of the zeros of
, respectively, as the minimum and maximum moduli of the zeros of 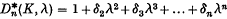 , the nth section of D*(K, λ).
, the nth section of D*(K, λ).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 70 , Issue 2 , September 1971 , pp. 257 - 262
- Copyright
- Copyright © Cambridge Philosophical Society 1971
References
REFERENCES
- 1
- Cited by


