Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T22:35:32.442Z Has data issue: false hasContentIssue false
  • English
  • Français

A lattice of extension rings for a commutative ring

Published online by Cambridge University Press:  24 October 2008

D. Kirby  and
M. R. Adranghi
D. Kirby
Affiliation:
University of Southampton
M. R. Adranghi
Affiliation:
University of Southampton
Get access Rights & Permissions [Opens in a new window]

Extract

The work of this note was motivated in the first place by North-cott's theory of dilatations for one-dimensional local rings (see, for example (4) and (5)). This produces a tree of local rings as in (4) which corresponds, in the abstract case, to the branching sequence of infinitely-near multiple points on an algebroid curve. From the algebraic point of view it seems more natural to characterize such one-dimensional local rings R by means of the set of rings which arise by blowing up all ideals Q which are primary for the maximal ideals M of R. This set of rings forms a lattice 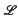(R), ordered by inclusion, each ring S of which is a finite R-module. Moreover the length of the R-module S/R is just the reduction number of the corresponding ideal Q (cf. theorem 1 of Northcott (6)). Thus the lattice 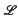(R) provides a finer classification of the rings R than does the set of reduction numbers (cf. Kirby (1)).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 84 , Issue 2 , September 1978 , pp. 225 - 234
Copyright
Copyright © Cambridge Philosophical Society 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Kirby, D.The defect of a one-dimensional local ring. Mathematika 6 (1959), 91–97.Google Scholar
(2)Kirby, D.A note on superficial elements of an ideal in a local ring. Quart. J. Math. Oxford (2) 14 (1963), 21–28.Google Scholar
(3)Matlis, E.The multiplicity and reduction number of a one-dimensional local ring. Proc. London Math. Soc. 26 (1ʘ73), 273–288.Google Scholar
(4)Northcott, D. G.The neighbourhoods of a local ring. J. London Math. Soc. 30 (1955), 360–375.CrossRefGoogle Scholar
(5)Northcott, D. G.On the notion of a first neighbourhood ring with an application to the AF + BΦ theorem. Proc. Cambridge Philos. Soc. 53 (1957), 43–56.Google Scholar
(6)Northcott, D. G.The reduction number of a one-dimensional local ring. Mathematika 6 (1959), 87–90.CrossRefGoogle Scholar
(7)Zariski, O. and Samuel, P.Commutative algebra, vo1. 1 (Princeton, van Nostrand, 1958).Google Scholar