Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Griffin, Phillip S.
1988.
Non-classical law of the iterated logarithm behaviour for trimmed sums.
Probability Theory and Related Fields,
Vol. 78,
Issue. 2,
p.
293.
Griffin, Philip S.
1988.
The influence of extremes on the law of the iterated logarithm.
Probability Theory and Related Fields,
Vol. 77,
Issue. 2,
p.
241.
Haeusler, Erich
and
Mason, David M.
1991.
Sums, Trimmed Sums and Extremes.
p.
355.
Csörgő, Sándor
Haeusler, Erich
and
Mason, David M.
1991.
Sums, Trimmed Sums and Extremes.
p.
215.
Maller, R. A.
1991.
Sums, Trimmed Sums and Extremes.
p.
179.
Egorov, V. A.
and
Pozdnyakov, V. I.
2000.
On the functional law of the iterated logarithm for trimmed sums.
Journal of Mathematical Sciences,
Vol. 99,
Issue. 2,
p.
1089.
Necir, Abdelhakim
2006.
A Nonparametric Sequential Test with Power 1 for the Mean of Lévy-stable Laws with Infinite Variance.
Methodology and Computing in Applied Probability,
Vol. 8,
Issue. 3,
p.
321.
Berkes, István
Horváth, Lajos
and
Schauer, Johannes
2011.
Asymptotics of trimmed CUSUM statistics.
Bernoulli,
Vol. 17,
Issue. 4,
BERKES, ISTVÁN
HORVÁTH, LAJOS
and
SCHAUER, JOHANNES
2012.
ASYMPTOTIC BEHAVIOR OF TRIMMED SUMS.
Stochastics and Dynamics,
Vol. 12,
Issue. 01,
p.
1150002.
Kesseböhmer, Marc
and
Schindler, Tanja
2019.
Strong Laws of Large Numbers for Intermediately Trimmed Sums of i.i.d. Random Variables with Infinite Mean.
Journal of Theoretical Probability,
Vol. 32,
Issue. 2,
p.
702.
Kesseböhmer, Marc
and
Schindler, Tanja
2019.
Strong laws of large numbers for intermediately trimmed Birkhoff sums of observables with infinite mean.
Stochastic Processes and their Applications,
Vol. 129,
Issue. 10,
p.
4163.
Kesseböhmer, Marc
and
Schindler, Tanja I.
2020.
Intermediately trimmed strong laws for Birkhoff sums on subshifts of finite type.
Dynamical Systems,
Vol. 35,
Issue. 2,
p.
275.
Kesseböhmer, Marc
and
Schindler, Tanja I
2020.
Mean convergence for intermediately trimmed Birkhoff sums of observables with regularly varying tails.
Nonlinearity,
Vol. 33,
Issue. 10,
p.
5543.
Bonanno, Claudio
and
Schindler, Tanja I.
2022.
Almost sure asymptotic behaviour of Birkhoff sums for infinite measure-preserving dynamical systems.
Discrete and Continuous Dynamical Systems,
Vol. 42,
Issue. 11,
p.
5541.
Bonanno, Claudio
and
Schindler, Tanja I.
2025.
Almost sure limit theorems with applications to non-regular continued fraction algorithms.
Stochastic Processes and their Applications,
Vol. 183,
Issue. ,
p.
104573.
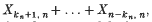 , where (kn)n ≥ 1 is a sequence of non-negative integers such that kn → ∞ and kn/n → 0 as n → ∞ at an appropriate rate, can be normalized and centred so that the law of the iterated logarithm holds. The method of proof is based on the almost sure properties of weighted uniform empirical processes.
, where (kn)n ≥ 1 is a sequence of non-negative integers such that kn → ∞ and kn/n → 0 as n → ∞ at an appropriate rate, can be normalized and centred so that the law of the iterated logarithm holds. The method of proof is based on the almost sure properties of weighted uniform empirical processes.