Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de la Bretèche, Régis
and
Tenenbaum, Gérald
2013.
Sur la conjecture de Manin pour certaines surfaces de Châtelet.
Journal of the Institute of Mathematics of Jussieu,
Vol. 12,
Issue. 4,
p.
759.
Tenenbaum, Gérald
2013.
Erdős Centennial.
Vol. 25,
Issue. ,
p.
651.
ELSHOLTZ, CHRISTIAN
and
TAO, TERENCE
2013.
COUNTING THE NUMBER OF SOLUTIONS TO THE ERDŐS–STRAUS EQUATION ON UNIT FRACTIONS.
Journal of the Australian Mathematical Society,
Vol. 94,
Issue. 1,
p.
50.
HENRIOT, KEVIN
2014.
Nair–Tenenbaum uniform with respect to the discriminant–ERRATUM.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 157,
Issue. 2,
p.
375.
Matomäki, Kaisa
and
Radziwiłł, Maksym
2015.
Sign changes of Hecke eigenvalues.
Geometric and Functional Analysis,
Vol. 25,
Issue. 6,
p.
1937.
Dartyge, Cécile
2015.
Le problème de Tchébychev pour le douzième polynôme cyclotomique.
Proceedings of the London Mathematical Society,
Vol. 111,
Issue. 1,
p.
1.
Tenenbaum, Gérald
2016.
Fonctions multiplicatives, sommes d’exponentielles, et loi des grands nombres.
Indagationes Mathematicae,
Vol. 27,
Issue. 2,
p.
590.
Goudout, Élie
2017.
Lois locales de la fonction ω dans presque tous les petits intervalles.
Proceedings of the London Mathematical Society,
Vol. 115,
Issue. 3,
p.
599.
Drappeau, Sary
2017.
Sums of Kloosterman sums in arithmetic progressions, and the error term in the dispersion method.
Proceedings of the London Mathematical Society,
Vol. 114,
Issue. 4,
p.
684.
Blomer, Valentin
2018.
Higher order divisor problems.
Mathematische Zeitschrift,
Vol. 290,
Issue. 3-4,
p.
937.
Ng, Nathan
and
Thom, Mark
2019.
Bounds and conjectures for additive divisor sums.
Functiones et Approximatio Commentarii Mathematici,
Vol. 60,
Issue. 1,
Drappeau, Sary
and
Topacogullari, Berke
2019.
Combinatorial identities and Titchmarsh’s
divisor problem for multiplicative functions.
Algebra & Number Theory,
Vol. 13,
Issue. 10,
p.
2383.
Matomäki, Kaisa
Radziwiłł, Maksym
and
Tao, Terence
2019.
Correlations of the von Mangoldt and higher divisor functions II: divisor correlations in short ranges.
Mathematische Annalen,
Vol. 374,
Issue. 1-2,
p.
793.
Matomäki, Kaisa
Radziwiłł, Maksym
and
Tao, Terence
2019.
Correlations of the von Mangoldt and higher divisor functions I. Long shift ranges.
Proceedings of the London Mathematical Society,
Vol. 118,
Issue. 2,
p.
284.
Browning, T. D.
and
Sofos, E.
2019.
Averages of arithmetic functions over principal ideals.
International Journal of Number Theory,
Vol. 15,
Issue. 03,
p.
547.
Matthiesen, Lilian
2020.
Linear correlations of multiplicative functions.
Proceedings of the London Mathematical Society,
Vol. 121,
Issue. 2,
p.
372.
Nelson, Paul D
2022.
Quadratic Hecke Sums and Mass Equidistribution.
International Mathematics Research Notices,
Vol. 2022,
Issue. 17,
p.
13659.
Huang, Bingrong
and
Lester, Stephen
2022.
Quantum variance for dihedral Maass forms.
Transactions of the American Mathematical Society,
Lichtman, Jared Duker
and
Teräväinen, Joni
2022.
On the Hardy–Littlewood–Chowla conjecture on average.
Forum of Mathematics, Sigma,
Vol. 10,
Issue. ,
Lichtman, Jared Duker
2022.
Averages of the Möbius Function on Shifted Primes.
The Quarterly Journal of Mathematics,
Vol. 73,
Issue. 2,
p.
729.


 [
[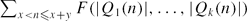 with an implicit dependency on the discriminant of
with an implicit dependency on the discriminant of 