Article contents
The natural ordering on a strictly real Banach algebra
Published online by Cambridge University Press: 24 October 2008
Abstract
A strictly real unital Banach algebra 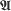 is one in which every element has real spectrum. An antilattice partial order and its associated open-interval topology are defined on
is one in which every element has real spectrum. An antilattice partial order and its associated open-interval topology are defined on 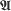 by taking as positive cone the principal component of the maximal group of the algebra, and their properties are studied. The topology coincides with the semimetric topology of the spectral radius, which is a seminorm, making
by taking as positive cone the principal component of the maximal group of the algebra, and their properties are studied. The topology coincides with the semimetric topology of the spectral radius, which is a seminorm, making 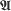 into a locally convex partially ordered topological algebra with continuous inversion and normal cone. Every positive element has a unique positive square root, and logarithm, and these functions and exp are continuous and monotone. The cone has the same closure in both open-interval and normal topologies, the closure being a wedge for an associated preorder on
into a locally convex partially ordered topological algebra with continuous inversion and normal cone. Every positive element has a unique positive square root, and logarithm, and these functions and exp are continuous and monotone. The cone has the same closure in both open-interval and normal topologies, the closure being a wedge for an associated preorder on 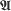 , this preorder coinciding with the preorder of Kelley and Vaught. The partial order and the associated preorder have the same dual cone. There is a modified Gelfand representation for (possibly non-commutative)
, this preorder coinciding with the preorder of Kelley and Vaught. The partial order and the associated preorder have the same dual cone. There is a modified Gelfand representation for (possibly non-commutative) 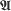 , and a boundary integral representation for functionals in the order dual. The compact convex subset in the dual is metrizable if the cone of the partial order in
, and a boundary integral representation for functionals in the order dual. The compact convex subset in the dual is metrizable if the cone of the partial order in 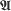 is separable.
is separable.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 107 , Issue 3 , May 1990 , pp. 539 - 556
- Copyright
- Copyright © Cambridge Philosophical Society 1990
References
REFERENCES
- 4
- Cited by


