No CrossRef data available.
A note concerning the global 2 -forms on a x = 0 threefold
Published online by Cambridge University Press: 24 October 2008
Extract
Let V be a smooth complex algebraic threefold with k(V) = 0. Consider the space of holomorphic 2-forms on V, and let s denote the rank of the subsheaf of 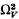 generated by these global forms. It was conjectured by Uenoin[8] that
generated by these global forms. It was conjectured by Uenoin[8] that 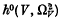 ≤ 3-here as always, hi denotes the dimension of the corresponding cohomology group Hi.
≤ 3-here as always, hi denotes the dimension of the corresponding cohomology group Hi.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 98 , Issue 2 , September 1985 , pp. 191 - 193
- Copyright
- Copyright © Cambridge Philosophical Society 1985
References
REFERENCES
[1]Kawamata, Y.. Elementary contractions of algebraic 3-folds. Annals of Math. 119 (1984), 95–110.CrossRefGoogle Scholar
[2]Kawamata, Y.. The cone of curves of algebraic varieties. Annals of Math. 119 (1984), 603–633.CrossRefGoogle Scholar
[3]Mabuchi, T.. Invariant η and uniruled threefolds. J. Math. Kyoto Univ. 22 (1982), 503–554.Google Scholar
[4]Miyaoka, Y.. The pseudo-effectivity of  for varieties with numerically effective canonical classes (To appear.)Google Scholar
for varieties with numerically effective canonical classes (To appear.)Google Scholar
[5]Mori, S.. Threefolds whose canonical bundles are not numerically effective. Annals of Math. 116 (1982), 133–176.CrossRefGoogle Scholar
[6]Reid, M.. Canonical 3-folds. In Journées de Géométrie Algébrique, Juillet 1979, ed. Beauville, A. (Sitjthoff and Noordhoff, 1980), pp. 273–310.Google Scholar
[7]Reid, M.. Minimal models of canonical threefolds. In Algebraic Varieties and Analytic Varieties, ed. Iitaka, S. and Morikawa, H., Advanced Studies in Pure Math., no. 1 (Kinokuniya and North-Holland, 1983), pp. 131–180.CrossRefGoogle Scholar
[8]Ueno, K.. Birational geometry of algebraic threefolds. In Journées de Géométrie Algébrique, Juillet 1979, ed. Beauville, A. (Sitjthoff and Noordhoff, 1980), pp. 311–323.Google Scholar
[9]Viehweg, E.. Klassifikationsheorie Algebraischer Varietäten der Dimension drei. Compositio Math. 41 (1980), 361–400.Google Scholar
[10]Wilson, P. M. H.. On regular threefolds with k = 0. Invent. math. 76 (1984), 345–355.CrossRefGoogle Scholar
[11]Wilson, P. M. H.. The components of mKv for threefolds with k(V) = 0. Math. Proc. Cambridge Philos. Soc. 97 (1985), 437–443.CrossRefGoogle Scholar


