A note on functions regular and bounded in the unit circle and small at a set of points near the circumference of the circle
Published online by Cambridge University Press: 24 October 2008
Extract
The following theorem was proved by Milloux:
Theorem A. Suppose that f (z) is regular and that | f(z) | < 1 in the unit circle. Suppose also that the set of points in the circle | z | ≤ r′ < 1 at which

cannot be enclosed in circles, the sum of whose radii is equal to 2eh−1. Then
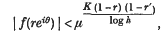
where K is a numerical constant.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 35 , Issue 3 , July 1939 , pp. 382 - 388
- Copyright
- Copyright © Cambridge Philosophical Society 1939
References
† Milloux, H., Mathematica, 4 (1930), 182–5.Google Scholar
† This theorem was suggested by a theorem of Hall, T. in his paper “Sur la mesure harmonique de certains ensembles”, Arkiv för Matematik, Astronomi och Fysik, 25 A, no. 28 (1937).Google Scholar Hall's theorem is concerned with functions regular and bounded in the half-plane R(z) > 0, and small at a set of points tending to the origin. This set may be as near as we please to the line R(z) = 0.
- 4
- Cited by


