Published online by Cambridge University Press: 24 October 2008
The Hopf-James invariants are a series of homomorphisms
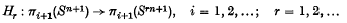
(see (3) or (13)). I. M. James (7) and H. Toda (13), have shown effectively that in the case n even and r a prime p the restrictions to the p-primary components may be embedded in exact sequences
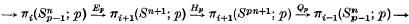
In this note we show that there are similar exact sequences if n is even and r = pq or if n is odd and r = 2pq, and we establish connexions in certain cases between the homomorphisms Hmn and the composite homomorphisms HmHn. We are able to compute the action of the invariants on the groups of the r-stem for r ≤ 9 with the partial exception of π6(S2) and π7(S2). The exact sequences yield useful criteria for determining the reduced product filtrations (see (9)) of elements.