Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dijksma, A.
and
de Snoo, H. S. V.
1974.
Distributional Watson Transforms.
SIAM Journal on Mathematical Analysis,
Vol. 5,
Issue. 6,
p.
888.
McBride, Adam C.
1978.
The Hankel transform of some classes of generalized functions and connections with fractional integration.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 81,
Issue. 1-2,
p.
95.
Duggal, B. P.
1978.
On Fourier transform type operators.
Periodica Mathematica Hungarica,
Vol. 9,
Issue. 1-2,
p.
55.
Duggal, B. P.
1979.
Functional equations and linear transformations, IIIB: Factorization.
Periodica Mathematica Hungarica,
Vol. 10,
Issue. 2-3,
p.
177.


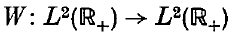 which satisfy
which satisfy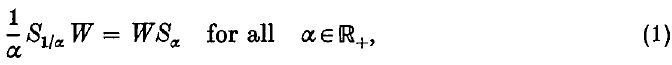
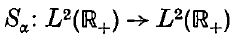 is defined by
is defined by