Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cochran, Tim D.
1989.
Localization and finiteness in link concordance.
Topology and its Applications,
Vol. 32,
Issue. 2,
p.
121.
Roßnagel, Alexander
Wedde, Peter
Hammer, Volker
and
Pordesch, Ulrich
1990.
Digitalisierung der Grundrechte?.
p.
118.
Cochran, T.D.
and
Levine, J.P.
1991.
Homology boundary links and the andrews–curtis conjecture.
Topology,
Vol. 30,
Issue. 2,
p.
231.
Farber, M.
1991.
Hermitian forms on link modules.
Commentarii Mathematici Helvetici,
Vol. 66,
Issue. 1,
p.
189.
Farber, Michael
1992.
Stable-homotopy and homology invariants of boundary links.
Transactions of the American Mathematical Society,
Vol. 334,
Issue. 1,
p.
455.
Farber, Michael
1992.
Noncommutative rational functions and boundary links.
Mathematische Annalen,
Vol. 293,
Issue. 1,
p.
543.
Levine, J.
Mio, W.
and
Orr, K. E.
1993.
Links with vanishing homotopy invariant.
Communications on Pure and Applied Mathematics,
Vol. 46,
Issue. 2,
p.
213.
Cochran, Tim D.
and
Orr, Kent E.
1994.
Homology boundary links and Blanchfield forms: concordance classification and new tangle-theoretic constructions.
Topology,
Vol. 33,
Issue. 3,
p.
397.
Bellis, Paul
1998.
Realizing homology boundary links with arbitrary patterns.
Transactions of the American Mathematical Society,
Vol. 350,
Issue. 1,
p.
87.
Cha, Jae
and
Ko, Ki
2005.
Signature invariants of covering links.
Transactions of the American Mathematical Society,
Vol. 358,
Issue. 8,
p.
3399.
CHA, JAE CHOON
2006.
THE EFFECT OF MUTATION ON LINK CONCORDANCE, 3-MANIFOLDS, AND THE MILNOR INVARIANTS.
Journal of Knot Theory and Its Ramifications,
Vol. 15,
Issue. 02,
p.
239.
FRIEDL, STEFAN
2006.
ALGORITHM FOR FINDING BOUNDARY LINK SEIFERT MATRICES.
Journal of Knot Theory and Its Ramifications,
Vol. 15,
Issue. 05,
p.
601.
LEVINE, JEROME
2007.
CONCORDANCE OF BOUNDARY LINKS.
Journal of Knot Theory and Its Ramifications,
Vol. 16,
Issue. 09,
p.
1111.
Cha, Jae Choon
and
Kim, Taehee
2008.
Covering link calculus and iterated Bing doubles.
Geometry & Topology,
Vol. 12,
Issue. 4,
p.
2173.
Harvey, Shelly L
2008.
Homology cobordism invariants and the Cochran–Orr–Teichner filtration of the link concordance group.
Geometry & Topology,
Vol. 12,
Issue. 1,
p.
387.
Cha, Jae Choon
and
Friedl, Stefan
2011.
Twisted torsion invariants and link concordance.
Forum Mathematicum,
p.
-.
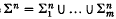 is the ordered disjoint union of m submanifolds of Sn+2, each homeomorphic to Sn. Σ is a boundary link if there is an oriented smooth submanifold Vn+1 of Sn+1,
is the ordered disjoint union of m submanifolds of Sn+2, each homeomorphic to Sn. Σ is a boundary link if there is an oriented smooth submanifold Vn+1 of Sn+1, 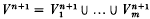 the disjoint union of the submanifolds
the disjoint union of the submanifolds 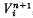 , such that ∂Vi = Σi (i = 1,…, m). A pair (Σ, V), where Σ is a boundary link and V as above, with each Vi connected (i = 1,…, m), is called an n-dimensional special Seifert pair. In this paper, we define a notion of cobordism of special Seifert pairs and give an algebraic description of the set (group) of cobordism classes.
, such that ∂Vi = Σi (i = 1,…, m). A pair (Σ, V), where Σ is a boundary link and V as above, with each Vi connected (i = 1,…, m), is called an n-dimensional special Seifert pair. In this paper, we define a notion of cobordism of special Seifert pairs and give an algebraic description of the set (group) of cobordism classes.

