Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jing, Yifan
Tran, Chieu-Minh
and
Zhang, Ruixiang
2023.
A nonabelian Brunn–Minkowski inequality.
Geometric and Functional Analysis,
Vol. 33,
Issue. 4,
p.
1048.

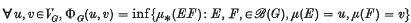
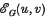 and we write ℰ
and we write ℰ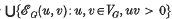 .
.