No CrossRef data available.
On pairs of additive forms modulo one
Published online by Cambridge University Press: 24 October 2008
Extract
Throughout this paper ∈ denotes an arbitrary positive number. For real α, ‖α‖ denotes the distance from α to the nearest integer. For natural numbers k we write K = 2k−1. In 1948 Heilbronn [8] showed that for any real α and N > C1(∈)
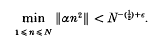
This theorem has since been generalized in many ways. In particular, results of the following type have been proved for natural numbers k ≥ 2, h = 1,2 and s.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 112 , Issue 3 , November 1992 , pp. 455 - 466
- Copyright
- Copyright © Cambridge Philosophical Society 1992
References
REFERENCES
[2]Baker, R. C. and Gajraj, J.. On the fractional parts of certain additive forms. Math. Proc. Cambridge Philos. Soc. 79 (1976), 463–467.CrossRefGoogle Scholar
[3]Baker, R. C. and Harman, G.. Small fractional parts of quadratic and additive forms. Math. Proc. Cambridge Philos. Soc. 90 (1981), 5–12.CrossRefGoogle Scholar
[4]Baker, R. C. and Schäffer, S.. Pairs of additive quadratic forms modulo one. Acta Arith., to appear.Google Scholar
[5]Cook, R. J.. The fractional parts of an additive form. Proc. Cambridge Philos. Soc. 72 (1972), 209–212.CrossRefGoogle Scholar
[6]Danicic, I.. Contributions to number theory. Ph.D. thesis, University of London (1957).Google Scholar
[7]Davenport, H.. On a theorem of Heilbronn. Quart. J. Math. Oxford Ser. (2) 18 (1967), 339–344.CrossRefGoogle Scholar
[8]Heilbronn, H.. On the distribution of the sequence θn2 (mod 1). Quart. J. Math. Oxford Ser. (2) 19 (1948), 249–256.CrossRefGoogle Scholar
[9]Liu, M.-C.. On the fractional parts of θnk and ønk. Quart. J. Math. Oxford Ser. (2) 21 (1970), 481–486.CrossRefGoogle Scholar
[10]Liu, M.-C.. Simultaneous approximation of two additive forms. Proc. Cambridge Philos. Soc. 75 (1974), 77–82.CrossRefGoogle Scholar
[11]Schlickewei, H.-P.. On indefinite diagonal forms in many variables. J. Reine Angew. Math. 307/308 (1979), 279–294.Google Scholar
[12]Schmidt, W. M.. Small Fractional Parts of Polynomials. Regional Conference series no. 32 (American Mathematical Society. 1977).Google Scholar

