No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Following Hardy and Titchmarsh(1) a function f(x) is said to be self-reciprocal if it satisfies the Fourier-Bessel integral transform
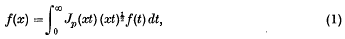
where Jp(x) is a Bessel function of order P ≥ –½. This integral is denoted by Rp. The special cases P ½ and P ½, we denote by Rs and Rc, respectively.