Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Collins, W. D.
1962.
On some triple series equations and their applications.
Archive for Rational Mechanics and Analysis,
Vol. 11,
Issue. 1,
p.
122.
Elwyn Williams, W.
1962.
The reduction of boundary value problems to Fredholm integral equations of the second kind.
Zeitschrift für angewandte Mathematik und Physik ZAMP,
Vol. 13,
Issue. 2,
p.
133.
Collins, W. D.
1962.
Some scalar diffraction problems for a spherical cap.
Archive for Rational Mechanics and Analysis,
Vol. 10,
Issue. 1,
p.
249.
Shail, Ronald
1963.
Hyperspherical caps in generalised axially symmetric potential theory (I).
Zeitschrift für angewandte Mathematik und Physik ZAMP,
Vol. 14,
Issue. 4,
p.
326.
Williams, W. E.
1963.
Note on the reduction of dual and triple series equations to dual and triple integral equations.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 59,
Issue. 4,
p.
731.
Williams, W. E.
1963.
A class of integral equations.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 59,
Issue. 3,
p.
589.
Thomas, D. P.
1963.
Diffraction by a spherical cap.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 59,
Issue. 1,
p.
197.
Noble, B.
1963.
Some dual series equations involving Jacobi polynomials.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 59,
Issue. 2,
p.
363.
Srivastav, R. P.
1963.
XVII.—Dual Series Relations. IV. Dual Relations Involving Series of Jacobi Polynomials.
Proceedings of the Royal Society of Edinburgh. Section A. Mathematical and Physical Sciences,
Vol. 66,
Issue. 3,
p.
185.
Collins, W. D.
1963.
A note on the axisymmetric Stokes flow of viscous fluid past a spherical cap.
Mathematika,
Vol. 10,
Issue. 1,
p.
72.
Williams, W. E.
1964.
The solution of dual series and dual integral equations.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 3,
p.
123.
Srivastava, K. N.
1967.
On Triple Series Equations Involving Series of Jacobi Polynomials.
Proceedings of the Edinburgh Mathematical Society,
Vol. 15,
Issue. 3,
p.
221.
Miles, John W.
1971.
Potential and Rayleigh-scattering theory for a spherical cap.
Quarterly of Applied Mathematics,
Vol. 29,
Issue. 1,
p.
109.
Jain, D. L.
and
Kanwal, R. P.
1972.
Three-part boundary value problems in potential and generalized axially symmetric potential theories.
Journal d'Analyse Mathématique,
Vol. 25,
Issue. 1,
p.
107.
Takagi, Hideaki
1974.
Slow Motion of a Spherical Cap in a Viscous Fluid. I. Uniform Translation and Rotation.
Journal of the Physical Society of Japan,
Vol. 37,
Issue. 1,
p.
229.
Kelman, Robert B.
and
Feinerman, Robert P.
1974.
Dual Orthogonal Series.
SIAM Journal on Mathematical Analysis,
Vol. 5,
Issue. 3,
p.
489.
Takagi, Hideaki
1974.
Slow Motion of a Spherical Cap in a Viscous Fluid. II. Free Suspension in a Shear Field.
Journal of the Physical Society of Japan,
Vol. 37,
Issue. 1,
p.
237.
Pasha, Mohammed Latif
1975.
Electrostatic potential due to a finite number of double laminae in free space.
Journal of Applied Physics,
Vol. 46,
Issue. 8,
p.
3368.
Vaid, B. K.
and
Jain, D. L.
1976.
Some Electrostatic and Hydrodynamic Problems for Two Spherical Caps.
SIAM Journal on Applied Mathematics,
Vol. 30,
Issue. 3,
p.
452.
Holdeman, L. B.
and
Holdeman, J. T.
1976.
Magnetic torque on a shielded superconducting gyroscope.
Journal of Applied Physics,
Vol. 47,
Issue. 11,
p.
4936.
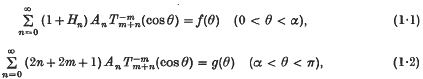 where
where  is the associated Legendre function of degree n + m and order −m of the first kind, Hn is a known coefficient of n, f(θ) and g(θ) are given functions of the variable θ and the equations are to be solved for the unknown coefficients An. In hydrodynamics, elasticity and electromagnetism such equations occur in many problems involving a spherical or spheroidal boundary when different conditions are prescribed on different parts of the boundary. These dual series equations are analogous to the dual integral equations which arise in the application of Hankel transforms to problems involving plane or paraboloidal boundaries, the theory and applications of these latter equations having been discussed by several writers amongst whom are Sneddon, Noble and Lebedev(1), (2), (3). The main result of this paper is that the solution of the dual series equations (1·1) and (1·2) for m a positive integer or zero can be reduced to the solution of a Fredholm integral equation of the second kind in one independent variable. The restriction that m be a positive integer or zero covers those dual series equations which arise in three-dimensional boundary-value problems but excludes those which arise in two-dimensional ones where m is
is the associated Legendre function of degree n + m and order −m of the first kind, Hn is a known coefficient of n, f(θ) and g(θ) are given functions of the variable θ and the equations are to be solved for the unknown coefficients An. In hydrodynamics, elasticity and electromagnetism such equations occur in many problems involving a spherical or spheroidal boundary when different conditions are prescribed on different parts of the boundary. These dual series equations are analogous to the dual integral equations which arise in the application of Hankel transforms to problems involving plane or paraboloidal boundaries, the theory and applications of these latter equations having been discussed by several writers amongst whom are Sneddon, Noble and Lebedev(1), (2), (3). The main result of this paper is that the solution of the dual series equations (1·1) and (1·2) for m a positive integer or zero can be reduced to the solution of a Fredholm integral equation of the second kind in one independent variable. The restriction that m be a positive integer or zero covers those dual series equations which arise in three-dimensional boundary-value problems but excludes those which arise in two-dimensional ones where m is  . These latter equations have, however, been discussed in a recent paper by Tranter (13).
. These latter equations have, however, been discussed in a recent paper by Tranter (13).