Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guo, Kanghui
1992.
On the spectral synthesis property and its application to partial differential equations.
Arkiv för Matematik,
Vol. 30,
Issue. 1-2,
p.
93.
Guo, Kanghui
1995.
A representation of distributions supported on smooth hypersurfaces of Rn.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 117,
Issue. 1,
p.
153.
Rosenblatt, Joseph
1995.
Linear independence of translations.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 59,
Issue. 1,
p.
131.
Puls, Michael J.
2019.
Sets of p-restriction and p-spectral synthesis.
Demonstratio Mathematica,
Vol. 52,
Issue. 1,
p.
397.

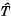 ε
ε