No CrossRef data available.
On the Phragmén-Lindelöf Principle
Published online by Cambridge University Press: 24 October 2008
Extract
In this short note my chief object is to prove the following theorem:
If
(1) f(z) is a regular function of z(= ρeiψ) in the angle |ψ| ≤ α, where 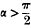 ;
;
(2) f(z)= 0(eαρ), where K is a positive constant, throughout this angle;
(3) f(z) is not identically zero;
then
(4) 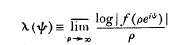
is a continuous function of ψ for |ψ| < α.
- Type
- Articles
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 25 , Issue 3 , July 1929 , pp. 265 - 267
- Copyright
- Copyright © Cambridge Philosophical Society 1929
References
* “On two theorems of F. Carlson and S. Wigert”, Acta Mathematica, vol. 42 (1920), pp. 327–339.CrossRefGoogle Scholar
† “Sur une extension d'un principe classique de l'analyse et sur quelques propriétés des fonctions monogènes dans le voisinage d'un point singulier”, Acta Mathematica, vol. 31 (1908), pp. 381–406.CrossRefGoogle Scholar
‡ Phragmén, and Lindelöf, , loc. cit. § 11.Google Scholar
§ Riesz, Marcel, “Sur le principe de Phragmén-Lindelöf”, Proc. Camb. Phil. Soc. vol. 20 (1920), pp. 205–207.Google Scholar
* In fact we can prove that λ(ψ) is continuous for ψ1 − δ ψ < ψ α, where δ is a positive number such that α − ψ1 + δ < π.Google Scholar
† Cf. Cramér, H., “Un théorèrae sur les séries de Dirichlet et son application”, Arkiv für Matematik, Astronomi och Fysik, t. 13, No. 22 (1918), p. 12.Google Scholar
‡ Compare this with a theorem of Persson, Paul, “Recherches sur une classe de fonctions entières”, Thèse, Upsal (1908), p. 8.Google ScholarPersson's Theorem is also cited on p. 36 of Carlson's thesis, “Sur une clause de séries de Taylor”, Upsal (1914).Google Scholar


