On Toda's fibrations
Published online by Cambridge University Press: 24 October 2008
Extract
In 1956 Toda [5] introduced two fibrations localized at p > 2:
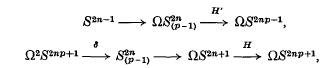
where 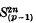 is a subcomplex of the James construction
is a subcomplex of the James construction 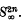 . The construction of H′ was somewhat difficult and was discussed by Moore (see [3]). Moore's definition however is not natural (in the sense of Theorem 1 (b) below). It is our purpose to give another definition, closer to Toda's original definition, which is natural, is an H map* and behaves well with respect to the Dyer-Lashof map λ: BΣp → Q(So). We use this to settle an unanswered question in [2].
. The construction of H′ was somewhat difficult and was discussed by Moore (see [3]). Moore's definition however is not natural (in the sense of Theorem 1 (b) below). It is our purpose to give another definition, closer to Toda's original definition, which is natural, is an H map* and behaves well with respect to the Dyer-Lashof map λ: BΣp → Q(So). We use this to settle an unanswered question in [2].
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 97 , Issue 2 , March 1985 , pp. 289 - 298
- Copyright
- Copyright © Cambridge Philosophical Society 1985
References
REFERENCES
- 11
- Cited by


