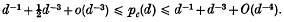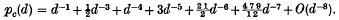Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sahimi, Muhammad
1983.
The Mathematics and Physics of Disordered Media: Percolation, Random Walk, Modeling, and Simulation.
Vol. 1035,
Issue. ,
p.
314.
Gaunt, D S
and
Brak, R
1984.
On the percolation threshold for a d-dimensional simple hypercubic lattice.
Journal of Physics A: Mathematical and General,
Vol. 17,
Issue. 8,
p.
1761.
Silva, J Kamphorst Leal da
and
Droz, M
1985.
Real-space renormalisation group for anisotropic directed bond percolation in arbitrary dimensions.
Journal of Physics C: Solid State Physics,
Vol. 18,
Issue. 4,
p.
745.
Kesten, Harry
1986.
École d'Été de Probabilités de Saint Flour XIV - 1984.
Vol. 1180,
Issue. ,
p.
125.
Grimmett, Geoffrey
1989.
Percolation.
p.
1.
Durrett, Rick
and
Swindle, Glen
1991.
Are there bushes in a forest?.
Stochastic Processes and their Applications,
Vol. 37,
Issue. 1,
p.
19.
Darling, R. W. R.
1991.
Lyapunov Exponents.
Vol. 1486,
Issue. ,
p.
206.
Nguyen, Bao Gia
and
Yang, Wei-Shih
1995.
Gaussian limit for critical oriented percolation in high dimensions.
Journal of Statistical Physics,
Vol. 78,
Issue. 3-4,
p.
841.
Marsili, Matteo
1996.
Directed polymers with killing.
Journal of Physics A: Mathematical and General,
Vol. 29,
Issue. 17,
p.
5405.
Benjamini, Itai
and
Kesten, Harry
1996.
Distinguishing sceneries by observing the scenery along a random walk path.
Journal d'Analyse Mathématique,
Vol. 69,
Issue. 1,
p.
97.
Piza, M. S. T.
1997.
Directed polymers in a random environment: Some results on fluctuations.
Journal of Statistical Physics,
Vol. 89,
Issue. 3-4,
p.
581.
Benjamini, Itai
Pemantle, Robin
and
Peres, Yuval
1998.
Unpredictable paths and percolation.
The Annals of Probability,
Vol. 26,
Issue. 3,
Jonasson, Johan
Mossel, Elchanan
and
Peres, Yuval
2000.
Percolation in a dependent random environment.
Random Structures and Algorithms,
Vol. 16,
Issue. 4,
p.
333.
Kesten, Harry
and
Su, Zhonggen
2000.
Some remarks on AB-percolation in high dimensions.
Journal of Mathematical Physics,
Vol. 41,
Issue. 3,
p.
1298.
Hofstad, Remco van der
and
Sakai, Akira
2005.
Critical points for spread-out self-avoiding walk, percolation and the contact process above the upper critical dimensions.
Probability Theory and Related Fields,
Vol. 132,
Issue. 3,
p.
438.
Sega, Gregor
2009.
Large-range constant threshold growth model in one dimension.
Electronic Journal of Probability,
Vol. 14,
Issue. none,
Lacoin, Hubert
2012.
Existence of an intermediate phase for oriented percolation.
Electronic Journal of Probability,
Vol. 17,
Issue. none,
Berger, Noam
and
Peres, Yuval
2013.
Detecting the trail of a random walker in a random scenery.
Electronic Journal of Probability,
Vol. 18,
Issue. none,
Balister, Paul
and
Bollobás, Béla
2014.
Interference percolation.
Random Structures & Algorithms,
Vol. 44,
Issue. 4,
p.
399.
Xue, Xiaofeng
2016.
Critical value for contact processes on clusters of oriented bond percolation.
Physica A: Statistical Mechanics and its Applications,
Vol. 448,
Issue. ,
p.
205.