Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T17:37:08.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Proof of the Brown–Erdős–Sós conjecture in groups

Part of: Abelian groups Graph theory

Published online by Cambridge University Press:  04 July 2019

RAJKO NENADOV ,
BENNY SUDAKOV  and
MYKHAYLO TYOMKYN
RAJKO NENADOV
Affiliation:
Department of Mathematics, ETH Zurich, Switzerland. e-mails: rnenadov@math.ethz.ch, benjamin.sudakov@math.ethz.ch
BENNY SUDAKOV
Affiliation:
Department of Mathematics, ETH Zurich, Switzerland. e-mails: rnenadov@math.ethz.ch, benjamin.sudakov@math.ethz.ch
MYKHAYLO TYOMKYN
Affiliation:
Mathematical Institute, University of Oxford, Oxford OX2 6GG. e-mail: tyomkyn@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The conjecture of Brown, Erdős and Sós from 1973 states that, for any k ≥ 3, if a 3-uniform hypergraph H with n vertices does not contain a set of k +3 vertices spanning at least k edges then it has o(n2) edges. The case k = 3 of this conjecture is the celebrated (6, 3)-theorem of Ruzsa and Szemerédi which implies Roth’s theorem on 3-term arithmetic progressions in dense sets of integers. Solymosi observed that, in order to prove the conjecture, one can assume that H consists of triples (a, b, ab) of some finite quasigroup Γ. Since this problem remains open for all k ≥ 4, he further proposed to study triple systems coming from finite groups. In this case he proved that the conjecture holds also for k = 4. Here we completely resolve the Brown–Erdős–Sós conjecture for all finite groups and values of k. Moreover, we prove that the hypergraphs coming from groups contain sets of size 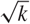$\Theta (\sqrt k )$ which span k edges. This is best possible and goes far beyond the conjecture.

MSC classification

Primary: 05C65: Hypergraphs
Secondary: 05C35: Extremal problems 20K01: Finite abelian groups
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 169 , Issue 2 , September 2020 , pp. 323 - 333
Copyright
© Cambridge Philosophical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

The first and the second author were supported in part by SNSF grant 200021-175573.

‡

Supported in part by ERC Starting Grant 633509 and ERC Starting Grant 676632.

References

REFERENCES

Ajtai, M. and Szemerédi, E.. Sets of lattice points that form no squares. Stud. Sci. Math. Hungar. 9 (1975), 9–11.Google Scholar
Angel, O., Benjamini, I. and Horesh., N.An isoperimetric inequality for planar triangulations. Discrete Comput. Geom. (2018), 1–8.Google Scholar
Brown, W., Erdős, P. and Sós., V.On the existence of triangulated spheres in 3-graphs, and related problems. Period. Math. Hungar. 3(3-4) (1973), 221–228.Google Scholar
Dodos, P., Kanellopoulos, V. and Tyros., K.A simple proof of the density Hales–Jewett theorem. Int. Math. Res. Not. (12) (2014), 3340–3352.CrossRefGoogle Scholar
Erdős, P., Frankl, P. and Rödl., V.The asymptotic number of graphs not containing a fixed subgraph and a problem for hypergraphs having no exponent. Graphs Combin., 2(1) (1986), 113–121.CrossRefGoogle Scholar
Erdős, P. and Straus, E.. How abelian is a finite group? Linear Multilinear Algebra 3(4) (1976), 307–312.CrossRefGoogle Scholar
Evans, T.. Embedding incomplete latin squares. Amer. Math. Monthly 67(10) (1960), 958–961.10.1080/00029890.1960.11992032CrossRefGoogle Scholar
Furstenberg, H. and Katznelson, Y.. An ergodic Szemerédi theorem for commuting transformations. J. Anal. Math. 34(1) (1978), 275–291.CrossRefGoogle Scholar
Furstenberg, H. and Katznelson, Y.. A density version of the Hales–Jewett theorem. J. Anal. Math. 57(1) (1991), 64–119.CrossRefGoogle Scholar
Gowers, W. T.. Hypergraph regularity and the multidimensional Szemerédi theorem. Ann. of Math. (2007), 897–946.10.4007/annals.2007.166.897CrossRefGoogle Scholar
Harper, L. H.. Global Methods for Combinatorial Isoperimetric Problems. Camb. Stud. Adv. Math. (Cambridge University Press, 2004).Google Scholar
Long, J.. A note on the Brown–Erdős–Sós conjecture in groups. Preprint (arXiv:1902.07693).Google Scholar
Polymath, D.. A new proof of the density Hales–Jewett theorem. Ann. of Math. (2012), 1283–1327.CrossRefGoogle Scholar
Pyber, L.. How abelian is a finite group? In The Mathematics of Paul Erdős I, pages 372–384 (Springer, 1997).Google Scholar
Rödl, V., Schacht, M., Tengan, E. and Tokushige., N.Density theorems and extremal hypergraph problems. Israel J. Math. 152(1) (2006), 371–380.CrossRefGoogle Scholar
Roth, K. F.. On certain sets of integers. J. Lond. Math. Soc. 1(1) (1953), 104–109.10.1112/jlms/s1-28.1.104CrossRefGoogle Scholar
Ruzsa, I. Z. and Szemerédi, E.. Triple systems with no six points carrying three triangles. Combinatorics (Keszthely, 1976), Coll. Math. Soc. J. Bolyai 18 (1978), 939–945.Google Scholar
Sárközy, G. N. and Selkow, S.. An extension of the Ruzsa–Szemerédi theorem. Combinatorica 25(1) (2004), 77–84.CrossRefGoogle Scholar
Solymosi, J.. Note on a generalisation of Roth’s theorem. In Discrete Comput. Geom., pages 825–827 (Springer, 2003).CrossRefGoogle Scholar
Solymosi, J.. The (7, 4)-conjecture in finite groups. Combin. Probab. Comput. 24(4) (2015), 680–686.CrossRefGoogle Scholar
Solymosi, J. and Wong, C.. The Brown–Erdős–Sós conjecture in finite abelian groups. arXiv:1901.10631.Google Scholar
Szemerédi, E.. On sets of integers containing no k elements in arithmetic progression. Acta Arith. 27 (1975), 199–245. Collection of articles in memory of Juriĭ Vladimirovič Linnik.CrossRefGoogle Scholar
Wong, C.. On the existence of dense substructures in finite groups. arXiv:1902.07819.Google Scholar