Rational normal octavic surfaces with a double line, in space of five dimensions: Addition
Published online by Cambridge University Press: 24 October 2008
Extract
In a recent paper in these Proceedings on the rational normal octavic surfaces with a double line in [5] I found four such surfaces, 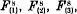 , and
, and 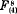 representable on a plane respectively by the systems of curves C5 (22, 19), C6(26, 14), and C7 (3, 28), with the base points in each case lying on an elliptic cubic. Inadvertently I overlooked a solution of certain indeterminate equations which leads to a fifth type
representable on a plane respectively by the systems of curves C5 (22, 19), C6(26, 14), and C7 (3, 28), with the base points in each case lying on an elliptic cubic. Inadvertently I overlooked a solution of certain indeterminate equations which leads to a fifth type 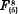 represented by the plane system C9(38, 1).
represented by the plane system C9(38, 1).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 3 , 30 July 1933 , pp. 405 - 406
- Copyright
- Copyright © Cambridge Philosophical Society 1933
References
* Babbage, , “Rational normal octavic surfaces with a double line, in space of five dimensions”, Proc. Camb. Phil. Soc., 29 (1933), 95–102.CrossRefGoogle Scholar
† Roth, , “On surfaces of sectional genus four”, Proc. Camb. Phil. Soc., 29 (1933), 184–194.CrossRefGoogle Scholar
- 1
- Cited by


