Reductions of ideals in local rings
Published online by Cambridge University Press: 24 October 2008
Extract
This paper contains some contributions to the analytic theory of ideals. The central concept is that of a reduction which is defined as follows: if 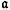 and
and 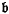 are ideals and
are ideals and 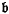 ⊆
⊆ 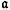 , then
, then 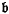 is called a reduction of
is called a reduction of 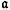 if
if 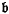
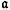 n =
n = 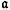 n+1 for all large values of n. The usefulness of the concept depends mainly on two facts. First, it defines a relationship between two ideals which is preserved under homomorphisms and ring extensions; secondly, what we may term the reduction process gets rid of superfluous elements of an ideal without disturbing the algebraic multiplicities associated with it. For example, the process when applied to a primary ideal belonging to the maximal ideal of a local ring gives rise to a system of parameters having the same multiplicity; but the methods work almost equally well for an arbitrary ideal and bring to light some interesting facts which are rather obscured in the special case. The concept seems to be suitable for a variety of applications. The present paper contains one instance which is a generalized form of the associative law for multiplicities (see § 8), and the authors hope to give other illustrations in a separate paper.
n+1 for all large values of n. The usefulness of the concept depends mainly on two facts. First, it defines a relationship between two ideals which is preserved under homomorphisms and ring extensions; secondly, what we may term the reduction process gets rid of superfluous elements of an ideal without disturbing the algebraic multiplicities associated with it. For example, the process when applied to a primary ideal belonging to the maximal ideal of a local ring gives rise to a system of parameters having the same multiplicity; but the methods work almost equally well for an arbitrary ideal and bring to light some interesting facts which are rather obscured in the special case. The concept seems to be suitable for a variety of applications. The present paper contains one instance which is a generalized form of the associative law for multiplicities (see § 8), and the authors hope to give other illustrations in a separate paper.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 50 , Issue 2 , April 1954 , pp. 145 - 158
- Copyright
- Copyright © Cambridge Philosophical Society 1954
References
REFERENCES
- 348
- Cited by


