Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Künzi, H.-P. A.
1986.
TOPOLOGICAL SPACES WITH A COARSEST COMPATIBLE QUASI-PROXIMITY.
Quaestiones Mathematicae,
Vol. 10,
Issue. 2,
p.
179.
Künzi, Hans-Peter A.
1989.
Some remarks on quasi-uniform spaces.
Glasgow Mathematical Journal,
Vol. 31,
Issue. 3,
p.
309.
Künzi, Hans-Peter A.
and
Ferrario, Nathalie
1991.
Bicompleteness of the fine quasi-uniformity.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 109,
Issue. 1,
p.
167.
KÜNZI, HANS‐PETER A.
1992.
Quasi Uniformities Defined by Sets of Neighborhoodsa.
Annals of the New York Academy of Sciences,
Vol. 659,
Issue. 1,
p.
125.
Schauerte, A.
1993.
On the MacNeille Completion of the Category of Partially Ordered Topological Spaces.
Mathematische Nachrichten,
Vol. 163,
Issue. 1,
p.
281.
Künzi, Hans-Peter A.
and
Watson, Stephen
1996.
A nontrivial T1-space admitting a unique quasi-proximity.
Glasgow Mathematical Journal,
Vol. 38,
Issue. 2,
p.
207.
Ivanov, A. A.
1996.
Bibliography on bitopological spaces. 2.
Journal of Mathematical Sciences,
Vol. 81,
Issue. 2,
p.
2497.
PIN, J.-E.
and
WEIL, P.
1999.
UNIFORMITIES ON FREE SEMIGROUPS.
International Journal of Algebra and Computation,
Vol. 09,
Issue. 03n04,
p.
431.
Salbany, S.
and
Romaguera, S.
2000.
DIEUDONN ÉCOMPLETE BISPACES.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 36,
Issue. 3-4,
p.
407.
Nailana, K. R.
2000.
Papers in Honour of Bernhard Banaschewski.
p.
445.
Romaguera, Salvador
2001.
ALMOST 2-FULLY NORMAL, PAIRWISE PARACOMPACT AND COMPLETE DEVELOPABLE BISPACES.
Quaestiones Mathematicae,
Vol. 24,
Issue. 1,
p.
21.
Künzi, H. P. A.
Romaguera, S.
and
Salbany, S.
2001.
Bispaces admitting only bicomplete or only totally bounded quasi-metrics.
Rendiconti del Circolo Matematico di Palermo,
Vol. 50,
Issue. 1,
p.
186.
Jung, Achim
Kegelmann, Mathias
and
Moshier, M.Andrew
2001.
Stably Compact Spaces and Closed Relations.
Electronic Notes in Theoretical Computer Science,
Vol. 45,
Issue. ,
p.
209.
Rodríguez-López, Jesús
and
Romaguera, Salvador
2002.
The relationship between the Vietoris topology and the Hausdorff quasi-uniformity.
Topology and its Applications,
Vol. 124,
Issue. 3,
p.
451.
2005.
Bitopological Spaces: Theory, Relations with Generalized Algebraic Structures, and Applications.
Vol. 199,
Issue. ,
p.
385.
Gerlo, A.
2008.
Approach Theory in a Category: A Study of Compactness and Hausdorff Separation.
Applied Categorical Structures,
Vol. 16,
Issue. 4,
p.
479.
Gerlo, A.
and
Vandersmissen, E.
2008.
Constructing the sobrification of an approach space via bicompletion.
Acta Mathematica Hungarica,
Vol. 120,
Issue. 1-2,
p.
39.
LAWSON, JIMMIE
2011.
Stably compact spaces.
Mathematical Structures in Computer Science,
Vol. 21,
Issue. 1,
p.
125.
Townsend, C. F.
2011.
The Patch Construction is Dual to Algebraic DCPO Representation.
Applied Categorical Structures,
Vol. 19,
Issue. 1,
p.
61.
Erné, Marcel
2018.
Categories of Locally Hypercompact Spaces and Quasicontinuous Posets.
Applied Categorical Structures,
Vol. 26,
Issue. 5,
p.
823.
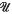 is a compatible totally bounded quasi-uniformity on a T0-space (X,
is a compatible totally bounded quasi-uniformity on a T0-space (X,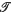 ), then the bicompletion
), then the bicompletion 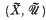 of (X,
of (X, 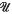 ) is a strongly sober, locally quasicompact space. It follows that the b-closure S of (X,
) is a strongly sober, locally quasicompact space. It follows that the b-closure S of (X, 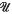 ) in
) in 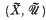 is homeomorphic to the sobrification of the space (X,
is homeomorphic to the sobrification of the space (X, 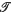 ). We prove that S is equal to
). We prove that S is equal to  if and only if (X,
if and only if (X, 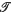 ) is a core-compact space in which every ultrafilter has an irreducible convergence set and
) is a core-compact space in which every ultrafilter has an irreducible convergence set and 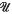 is the coarsest quasi-uniformity compatible with
is the coarsest quasi-uniformity compatible with 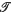 . If
. If 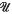 is the Pervin quasi-uniformity on X, then S is equal to
is the Pervin quasi-uniformity on X, then S is equal to  if and only if X is hereditarily quasicompact, or equivalently,
if and only if X is hereditarily quasicompact, or equivalently, 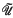 is the Pervin quasi-uniformity on
is the Pervin quasi-uniformity on  .
.