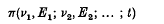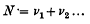Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bartlett, M. S.
and
Kendall, David G.
1951.
On the use of the characteristic functional in the analysis of some stochastic processes occurring in physics and biology.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 47,
Issue. 1,
p.
65.
Bartlett, M. S.
1951.
The dual recurrence relation for multiplicative processes.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 47,
Issue. 4,
p.
821.
Ramakrishnan, Alladi
1952.
A note on Janossy's mathematical model of a nucleon cascade.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 48,
Issue. 3,
p.
451.
Messel, H
and
Potts, R B
1952.
Note on the Fluctuation Problem in Cascade Theory.
Proceedings of the Physical Society. Section A,
Vol. 65,
Issue. 10,
p.
854.
Ramakrishnan, Alladi
1953.
Stochastic processes associated with random divisions of a line.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 49,
Issue. 3,
p.
473.
Ramakrishnan, Alladi
and
Srinivasan, S. K.
1956.
A new approach to the cascade theory.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 44,
Issue. 5,
p.
263.
Ramakrishnan, Alladi
and
Srinivasan, S. K.
1957.
A note on cascade theory with ionisation loss.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 45,
Issue. 2,
p.
133.
Ramakrishnan, Alladi
and
Srinivasan, S. K.
1958.
On age distribution in population growth.
The Bulletin of Mathematical Biophysics,
Vol. 20,
Issue. 4,
p.
289.
Ramakrishnan, Alladi
1959.
Prinzipien der Thermodynamik und Statistik / Principles of Thermodynamics and Statistics.
Vol. 2 / 3 / 2,
Issue. ,
p.
524.
Gardner, J. W.
1960.
Markoff cascades with general source terms.
Il Nuovo Cimento,
Vol. 16,
Issue. 6,
p.
977.
Ranganathan, N R
and
Vasudevan, R
1960.
The Stochastic Problem of Electron-Photon Cascades including Polarization.
Proceedings of the Physical Society,
Vol. 76,
Issue. 5,
p.
650.
Gardner, J. W.
1960.
The characteristic-functional method in cascade theory.
Il Nuovo Cimento,
Vol. 17,
Issue. 2,
p.
205.
Ramakrishnan, Alladi
and
Radha, T. K.
1961.
Correlation problems in evolutionary stochastic processess.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 57,
Issue. 4,
p.
843.
Moyal, J. E.
1962.
The general theory of stochastic population processes.
Acta Mathematica,
Vol. 108,
Issue. 0,
p.
1.
Locher, Milan P.
1963.
On the combinatorial derivation of the coefficients in the product density method.
Zeitschrift für angewandte Mathematik und Physik ZAMP,
Vol. 14,
Issue. 4,
p.
368.
Srinivasan, S. K.
and
Iyer, K. S. S.
1964.
Sequent correlations in evolutionary stochastic point processes and its application to cascade theories.
Il Nuovo Cimento,
Vol. 33,
Issue. 2,
p.
273.
Lewis, T.
and
Govier, L. J.
1964.
Some Properties of Counts of Events for Certain Types of Point Process.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 26,
Issue. 2,
p.
325.
SAITO, Keiichi
and
OTSUKA, Masuhiko
1965.
Theory of Statistical Fluctuations in Neutron Distributions.
Journal of Nuclear Science and Technology,
Vol. 2,
Issue. 8,
p.
304.
Srinivasaw, S. K.
1965.
A novel approach to the theory of shot noise.
Il Nuovo Cimento,
Vol. 38,
Issue. 2,
p.
979.
Srinivasan, S. K.
1967.
Symposia on Theoretical Physics 4.
p.
143.