Summability fields which span the bounded sequences
Published online by Cambridge University Press: 24 October 2008
Extract
If A = (am, n) is a regular matrix, then for any sequence x = {xn}, Am(x) will denote the transform 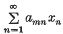 and A-lim x denotes
and A-lim x denotes 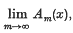 if that limit exists. We shall denote by
if that limit exists. We shall denote by 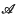 the set of bounded sequences which are summed by A. If B is another regular matrix with
the set of bounded sequences which are summed by A. If B is another regular matrix with 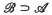 then we say that B is b-stronger than A. In that case B must be b-consistent with A (see (4) and (6)), i.e. if
then we say that B is b-stronger than A. In that case B must be b-consistent with A (see (4) and (6)), i.e. if 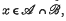 then
then
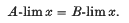
If {μn} is a sequence of positive real numbers with 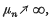 we say that A and B are (μn)-consistent if every sequencer x = {xn} satisfying xn = 0(μn) which is summed by both A and B is summed to the same value by both matrices. A finite set of matrices A1, A2, …, AN is said to be simultaneously (μn)-inconsistent (b-consistent) if whenever
we say that A and B are (μn)-consistent if every sequencer x = {xn} satisfying xn = 0(μn) which is summed by both A and B is summed to the same value by both matrices. A finite set of matrices A1, A2, …, AN is said to be simultaneously (μn)-inconsistent (b-consistent) if whenever 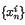 is summed by Ai with
is summed by Ai with 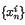 (i = l, 2, …, N) then
(i = l, 2, …, N) then 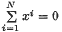 implies that
implies that 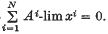 The set of sequences,
The set of sequences, 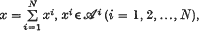 is denoted by
is denoted by 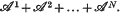
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 63 , Issue 1 , January 1967 , pp. 99 - 106
- Copyright
- Copyright © Cambridge Philosophical Society 1967
References
REFERENCES
- 1
- Cited by


