No CrossRef data available.
Published online by Cambridge University Press: 17 June 2022
A handlebody link is a union of handlebodies of positive genus embedded in 3-space, which generalises the notion of links in classical knot theory. In this paper, we consider handlebody links with a genus two handlebody and
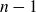 $n-1$
solid tori,
$n-1$
solid tori,
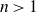 $n>1$
. Our main result is the classification of such handlebody links with six crossings or less, up to ambient isotopy.
$n>1$
. Our main result is the classification of such handlebody links with six crossings or less, up to ambient isotopy.