No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
1. Published tables facilitating the numerical evaluation of the definite integral
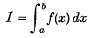
from given numerical values f(xi) of the integrand in the form of a weighted sum
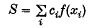
essentially deal with the following situations:
(a) The arguments xi are equidistant, i.e. xi = x0+iw; i=integer and the weight coefficients ci are tabulated for all arguments xi occurring in the summation. Among these tables the most important are:
(a1) panels in which the end-points of the integration a and b are two of the xi, and in particular
(a11) panels confined to the range of the integration in which
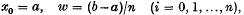
(a12) panels extending beyond the range of integration which usually have the same number of arguments, k, below a and beyond b, so that
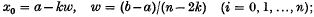
(a2) panels in which a and b are at distance ½w from one of the xi, and in particular
(a21) panels confined to the range of integration in which
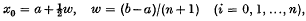
(a22) panels extending beyond the range of integration which usually have the same number of (k) points below a and beyond b, so that
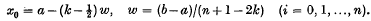
(b) The n arguments xi are not equidistant but are specially chosen so that for a given n the sum S approximates to I with highest precision. Gauss's formula (see, for example, Milne-Thomson (4)) and various formulae of approximate product integration (see, for example, Beard (l)) are examples of these. In Chebyshev's integration formula (see, for example, Runge and König (5)) the xi required for equal weights ctare used, resulting in an important formula when the ordinates f(xi) are affeected by observational errors of equal variance.