Article contents
A theorem on positive harmonic functions
Published online by Cambridge University Press: 24 October 2008
Extract
1. Let z = reiθ, and let h(z) denote a (regular) positive harmonic function in the unit circle r < 1. Then h(r) (1−r) and h(r)/(1 − r) tend to limits as r → 1. The first limit is finite; the second may be infinite. Such properties of h can be obtained in a straightforward way by using the fact that we can write
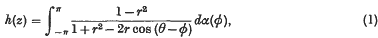
where α(phgr) is non-decreasing in the closed interval (− π, π). Another method is to write
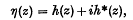
where h* is a harmonic function conjugate to h. Then the function
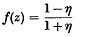
has the property | f | < 1 in the unit circle. Such functions have been studied by Julia, Wolff, Carathéodory and others.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 45 , Issue 2 , April 1949 , pp. 207 - 212
- Copyright
- Copyright © Cambridge Philosophical Society 1949
- 2
- Cited by


