Article contents
Topos points of quasi-coherent sheaves over monoid schemes
Published online by Cambridge University Press: 11 March 2019
Abstract
Let X be a monoid scheme. We will show that the stalk at any point of X defines a point of the topos 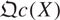 of quasi-coherent sheaves over X. As it turns out, every topos point of
of quasi-coherent sheaves over X. As it turns out, every topos point of 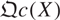 is of this form if X satisfies some finiteness conditions. In particular, it suffices for M/M× to be finitely generated when X is affine, where M× is the group of invertible elements.
is of this form if X satisfies some finiteness conditions. In particular, it suffices for M/M× to be finitely generated when X is affine, where M× is the group of invertible elements.
This allows us to prove that two quasi-projective monoid schemes X and Y are isomorphic if and only if 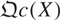 and
and 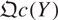 are equivalent.
are equivalent.
The finiteness conditions are essential, as one can already conclude by the work of A. Connes and C. Consani [3]. We will study the topos points of free commutative monoids and show that already for ℕ∞, there are ‘hidden’ points. That is to say, there are topos points which are not coming from prime ideals. This observation reveals that there might be a more interesting ‘geometry of monoids’.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 169 , Issue 1 , July 2020 , pp. 31 - 74
- Copyright
- © Cambridge Philosophical Society 2019
References
REFERENCES
- 2
- Cited by


