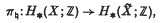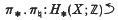Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Iriye, Kouyemon
and
Kono, Akira
1985.
Modp retracts ofG-product spaces.
Mathematische Zeitschrift,
Vol. 190,
Issue. 3,
p.
357.
Dold, Albrecht
1986.
Ramified coverings, orbit projections and symmetric powers.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 99,
Issue. 1,
p.
65.
Farjoun, E. Dror
1989.
A transfer map for singular fibrations.
Israel Journal of Mathematics,
Vol. 66,
Issue. 1-3,
p.
132.
Cohen, F. R.
Cohen, R. L.
Mann, B. M.
and
Milgram, R. J.
1993.
The homotopy type of rational functions.
Mathematische Zeitschrift,
Vol. 213,
Issue. 1,
p.
37.
Pejsachowicz, Jacobo
and
Skiba, Robert
2005.
Handbook of Topological Fixed Point Theory.
p.
217.
Aguilar, Marcelo A.
and
Prieto, Carlos
2006.
Transfers for ramified covering maps in homology and cohomology.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2006,
Issue. 1,
BUCHSTABER, V. M.
BUCHSTABER, V. M.
and
REES, E. G.
2008.
Frobenius n-homomorphisms, transfers and branched coverings.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 144,
Issue. 1,
p.
1.
Aguilar, Marcelo A.
and
Prieto, Carlos
2008.
Simplicial ramified covering maps.
Topology and its Applications,
Vol. 156,
Issue. 2,
p.
205.
Aguilar, Marcelo A.
and
Prieto, Carlos
2010.
The transfer for ramified covering G-maps.
Forum Mathematicum,
Vol. 22,
Issue. 6,
Neretin, Yu. A.
2010.
On spherical functions on the group SU(2) × SU(2) × SU(2).
Functional Analysis and Its Applications,
Vol. 44,
Issue. 1,
p.
48.
Aguilar, Marcelo A.
and
Prieto, Carlos
2010.
Bredon homology and ramified covering G-maps.
Topology and its Applications,
Vol. 157,
Issue. 2,
p.
401.
Natanzon, S. M.
2010.
Simple Hurwitz numbers of a disk.
Functional Analysis and Its Applications,
Vol. 44,
Issue. 1,
p.
36.
Натанзон, Сергей Миронович
Natanzon, Sergey Mironovich
Натанзон, Сергей Миронович
Natanzon, Sergey Mironovich
Натанзон, Сергей Миронович
Natanzon, Sergey Mironovich
Натанзон, Сергей Миронович
and
Natanzon, Sergey Mironovich
2010.
Дисковые одинарные числа Гурвица.
Функциональный анализ и его приложения,
Vol. 44,
Issue. 1,
p.
44.
Menet, Grégoire
2015.
Beauville–Bogomolov lattice for a singular symplectic variety of dimension 4.
Journal of Pure and Applied Algebra,
Vol. 219,
Issue. 5,
p.
1455.
Gugnin, Dmitry Vladimirovich
2018.
О нижних оценках на степень разветвленных накрытий многообразий.
Математические заметки,
Vol. 103,
Issue. 2,
p.
186.
Gugnin, D. V.
2018.
Lower Bounds for the Degree of a Branched Covering of a Manifold.
Mathematical Notes,
Vol. 103,
Issue. 1-2,
p.
187.
Menet, Grégoire
2018.
On the integral cohomology of quotients of manifolds by cyclic groups.
Journal de Mathématiques Pures et Appliquées,
Vol. 119,
Issue. ,
p.
280.
BOOTE, YUMI
and
RAY, NIGEL
2018.
ON THE SYMMETRIC SQUARES OF COMPLEX AND QUATERNIONIC PROJECTIVE SPACE.
Glasgow Mathematical Journal,
Vol. 60,
Issue. 3,
p.
703.
Costa, Antonio F.
and
Porto, Ana M.
2019.
Note on topologically singular points in the moduli space of Riemann surfaces of genus 2.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 113,
Issue. 4,
p.
3375.
Gugnin, Dmitry Vladimirovich
2019.
Разветвленные накрытия многообразий и $\boldsymbol{nH}$-пространства.
Функциональный анализ и его приложения,
Vol. 53,
Issue. 2,
p.
68.